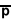Symbole de Wythoff - Définition
La liste des auteurs de cet article est disponible ici.
Description
Les lettres p,q,r représentent la forme du triangle fondamental pour la symétrie, plus précisément chaque nombre est le nombre de miroirs réflexifs qui existent à chaque sommet. Sur la sphère, il existe trois types principaux de symétries : (3 3 2), (4 3 2), (5 3 2) et une famille infinie (p 2 2), pour p=2,3,... quelconque (toutes les familles simples ont un angle droit, donc r=2)
La position de la barre verticale dans le symbole est utilisée pour indiquer des formes spécifiques (une position de catégorie du point générateur) dans le triangle fondamental. Le point générateur peut être soit sur ou à côté de chaque miroir, activé ou non. Cette distinction engendre 8 (2³) formes possibles, négligeant une où le point générateur est sur tous les miroirs.
Dans cette notation, les miroirs sont étiquetés pr l'ordre de réflexion du sommet opposé. Les valeurs p,q,r sont listées avant la barre si le miroir correspondant est actif.
Le symbole impossible | p q r, qui implique le point générateur est sur tous les miroirs qui est le seul possible si le triangle est généré en un point. Ce symbole inusité est réassigné pour signifier quelque chose de différent. Ces symboles représentent le cas où tous les miroirs sont actifs, mais les images réfléchies énumérées de manière impaire sont ignorées. Ceci engendre des résultats de symétrie rotationnelle.
Ce symbole est fonctionnellement similaire au diagramme de Coxeter-Dynkin plus général qui montre un triangle marqué p, q, r sur les arêtes, et des cercles sur les noeuds, représentant les miroirs pour impliquer si le point générateur touchait ce miroir (le diagramme de Coxeter-Dynkin est montré comme un graphe linéaire lorsque r=2 puisqu'il n'y a pas de réflexions interagissant à travers un angle droit).
Résumé des pavages sphériques et plans
Une sélection des pavages créés par la construction de Wythoff sont donnés ci-dessous.
Les pavages sphériques (r=2)
| (p q 2) | Triangle fondamental | Parent | Tronqué | Rectifié | Bitronqué | Birectifié (dual) | Biseauté | Omnitronqué () | Adouci |
|---|---|---|---|---|---|---|---|---|---|
| Symbole de Wythoff | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Symbole de Schläfli | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Diagramme de Coxeter-Dynkin |
|
|
|
|
|
|
|
| |
| Figure de sommet | pq | (q.2p.2p) | (p.q.p.q) | (p.2q.2q) | qp | (p.4.q.4) | (4.2p.2q) | (3.3.p.3.q) | |
| Tetraèdrique (3 3 2) | 72px | 64px {3,3} | 64px (3.6.6) | 64px (3.3a.3.3a) | 64px (3.6.6) | 64px {3,3} | 64px (3a.4.3b.4) | 64px (4.6a.6b) | 64px (3.3.3a.3.3b) |
| Octaèdrique (4 3 2) |
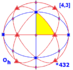
| 64px {4,3} | 64px (3.8.8) | 64px (3.4.3.4) | 64px (4.6.6) | 64px {3,4} | 64px (3.4.4a.4) | 64px (4.6.8) | 65px (3.3.3a.3.4) |
| Icosaèdrique (5 3 2) |
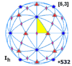
| 64px {5,3} | 64px (3.10.10) | 64px (3.5.3.5) | 64px (5.6.6) | 64px {3,5} | 64px (3.4.5.4) |

(4.6.10) | 64px (3.3.3a.3.5) |
Pavages planaires (r=2)
Un pavage hyperbolique représentatif est donné, et montré comme une projection de disque de Poincaré.
| (p q 2) | Triangle fondamental | Parent | Tronqué | Rectifié | Bitronqué | Birectifié (dual) | Biseauté | Omnitronqué () | Adouci |
|---|---|---|---|---|---|---|---|---|---|
| Symbole de Wythoff | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Symbole de Schläfli | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Diagramme de Coxeter-Dynkin |
|
|
|
|
|
|
|
| |
| Figure de sommet | pq | (q.2p.2p) | (p.q.p.q) | (p.2q.2q) | qp | (p.4.q.4) | (4.2p.2q) | (3.3.p.3.q) | |
| Pavage carré (4 4 2) |
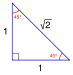
|

{4,4} |

4.8.8 | 64px 4.4a.4.4a | 64px 4.8.8 | 64px {4,4} | 64px 4.4a.4b.4a | 64px 4.8.8 |

3.3.4a.3.4b |
| (Plan hyperbolique) (5 4 2) | 64px {5,4} | 64px 4.10.10 | 64px 4.5.4.5 | 64px 5.8.8 | 64px {4,5} | 64px 4.4.5.4 | 64px 4.8.10 | 3.3.4.3.5 | |
| Pavage hexagonal (6 3 2) |
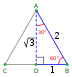
|

{6,3} |

3.12.12 |

3.6.3.6 | 64px 6.6.6 |

{3,6} |

3.4.6.4 |

4.6.12 |

3.3.3.3.6 |
| (Plan hyperbolique) (7 3 2) |

{7,3} |

3.14.14 |

3.7.3.7 | 64px 7.6.6 |

{3,7} | 64px 3.4.7.4 |

4.6.14 | 65px 3.3.3.3.7 |
Pavages planaires (r>2)
Le diagramme de Coxeter-Dynkin est donné dans une forme linéaire, bien que ce soit un triangle, avec le segment r trainant connecté au premier noeud.
| Symbole de Wythoff (p q r) | Triangle fondamental | q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Diagramme de Coxeter-Dynkin |
|
|
|
|
|
|
|
| |
| Figure de sommet | (p.q)r | (r.2p.q.2p) | (p.r)q | (q.2r.p.2r) | (q.r)p | (q.2r.p.2r) | (r.2q.p.2q) | (3.r.3.q.3.p) | |
| Triangulaire (3 3 3) |
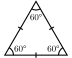
| 64px (3.3)3 | 64px 3.6.3.6 | 64px (3.3)3 | 64px 3.6.3.6 | 64px (3.3)3 | 64px 3.6.3.6 | 64px 6.6.6 | 64px 3.3.3.3.3.3 |
| Hyperbolique (4 3 3) | 64px (3.4)³ | 64px 3.8.3.8 | 64px (3.4)³ | 64px 3.6.4.6 | 64px (3.3)4 | 64px 3.6.4.6 | 64px 6.6.8 | 3.3.3.3.3.4 |
Recouvrements des pavages sphériques (r=2)
Les pavages sont montrés comme des polyèdres. Certaines de ces formes sont dégénérées, données par des accolades des figures de sommet, avec les arêtes ou les sommets de recouvrement.
| (p q 2) | Triangle fondamental | Parent | Tronqué | Rectifié | Bitronqué | Birectifié (dual) | Biseauté | Omnitronqué () | Adouci |
|---|---|---|---|---|---|---|---|---|---|
| Symbole de Wythoff | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Symbole de Schläfli | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Diagramme de Coxeter-Dynkin |
|
|
|
|
|
|
|
| |
| Figure de sommet | pq | (q.2p.2p) | (p.q.p.q) | (p.2q.2q) | qp | (p.4.q.4) | (4.2p.2q) | (3.3.p.3.q) | |
| Icosaèdrique (5/2 3 2) |

{3,5/2} |

(5/2.6.6) |

(3.5/2)2 |

[3.10/2.10/2] |

{5/2,3} | 64px [3.4.5/2.4] | 64px [4.10/2.6] |

(3.3.3.3.5/2) | |
| Icosaèdrique (5 5/2 2) |

{5,5/2} |
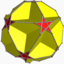
(5/2.10.10) |

(5/2.5)2 |

[5.10/2.10/2] |

{5/2,5} | 64px (5/2.4.5.4) | 64px [4.10/2.10] |

(3.3.5/2.3.5) |