Symbole de Wythoff - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie, un symbole de Wythoff est une notation courte, créée par le mathématicien Willem Abraham Wythoff, pour nommer les polyèdres réguliers et semi-réguliers utilisant une construction kaléidoscopique, en les représentant comme des pavages sur la surface d'une sphère, sur un plan euclidien ou un plan hyperbolique.
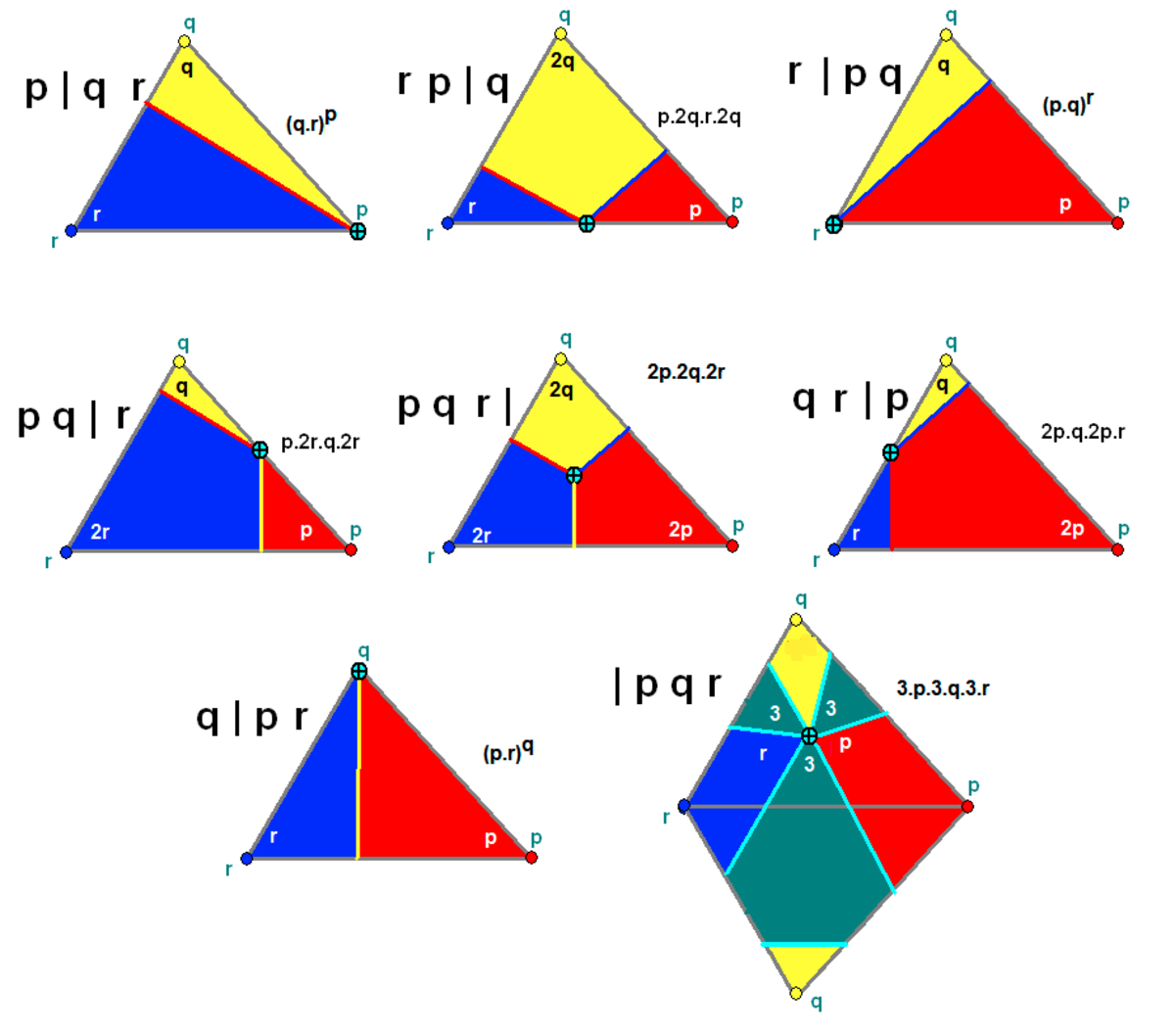
Le symbole de Wythoff donne 3 nombres p,q,r et une barre verticale positionnelle (|) qui sépare les nombres avant et après elle. Chaque nombre représente l'ordre des miroirs à un sommet du triangle fondamental.
Chaque symbole représente un polyèdre uniforme ou un pavage, bien qu'un même polyèdre/pavage puisse avoir des symboles de Wythoff différents à partir de générateurs symétriques différents. Par exemple, le cube régulier peut être représenté par 3 | 4 2 avec une symétrie Oh et 2 4 | 2 comme un prisme carré avec deux couleurs et une symétrie D4h, autant que 2 2 2 | avec 3 couleurs et une symétrie D2h.
Tableau de résumé
Il existe 7 points générateurs avec chaque ensemble de p,q,r : (et quelques formes particulières)
| Général | Triangle droit (r=2) | |||
|---|---|---|---|---|
| Description | Symbole de Wythoff | Configuration de sommet | Symbole de Wythoff | Configuration de sommet |
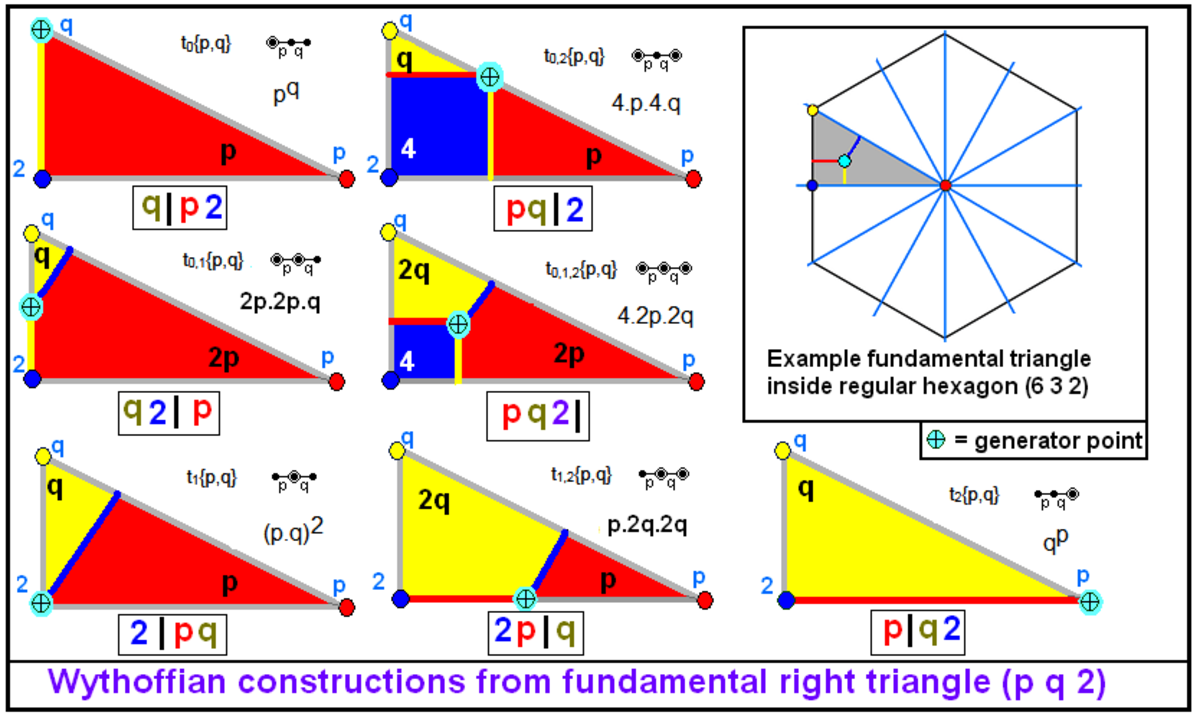
| régulier et quasi-régulier | q | p r | (p.r)q | q | p 2 | pq |
| p | q r | (q.r)p | p | q 2 | qp | |
| r | p q | (q.p)r | 2 | p q | (q.p)² | |
| tronqué et développé | q r | p | q.2p.r.2p | q 2 | p | q.2p.2p |
| p r | q | p.2q.r.2q | p 2 | q | p.2q.2q | |
| p q | r | 2r.q.2r.p | p q | 2 | 4.q.4.p | |
| faces paires | p q r | | 2r.2q.2p | p q 2 | | 4.2q.2p |
| p q (r s) | | 2p.2q.-2p.-2q | p 2 (r s) | | 2p.4.-2p.4/3 | |
| adouci | | p q r | 3.r.3.q.3.p | | p q 2 | 3.3.q.3.p |
| | p q r s | (4.p.4.q.4.r.4.s)/2 | - | - | |
Il existe trois cas particuliers :
- p q (r s) | - C'est un mélange de p q r | et p q s |.
- | p q r - Les formes adoucies (alternées) donnent cet autre symbole inhabituel.
- | p q r s - Une forme unique adoucie pour le U75 qui n'est pas constructible au sens de Wythoff.
Les triangles de symétrie
Il existe 4 classes de symétrie de réflexions sur la sphère, et 2 pour le plan euclidien et infiniment beaucoup pour le plan hyperbolique, les premières :
- (p 2 2) symétrie dièdrique p=2,3,4... (Ordre 4p)
- (3 3 2) symétrie tétraédrique (Ordre 24)
- (4 3 2) symétrie octaèdrique (Ordre 48)
- (5 3 2) symétrie icosaèdrique (Ordre 120)
- (4 4 2) - symétrie *442 - Triangle 45-45-90 (inclut le domaine carré (2 2 2 2))
- (3 3 3) - symétrie *333 - Triangle 60-60-60
- (6 3 2) - symétrie *632 - Triangle 30-60-90
- (7 3 2) - symétrie *732 (plan hyperbolique)
| Sphérique dièdrique | Sphérique | |||
|---|---|---|---|---|
| D2h | D3h | Td | Oh | Ih |
| *222 | *322 | *332 | *432 | *532 |
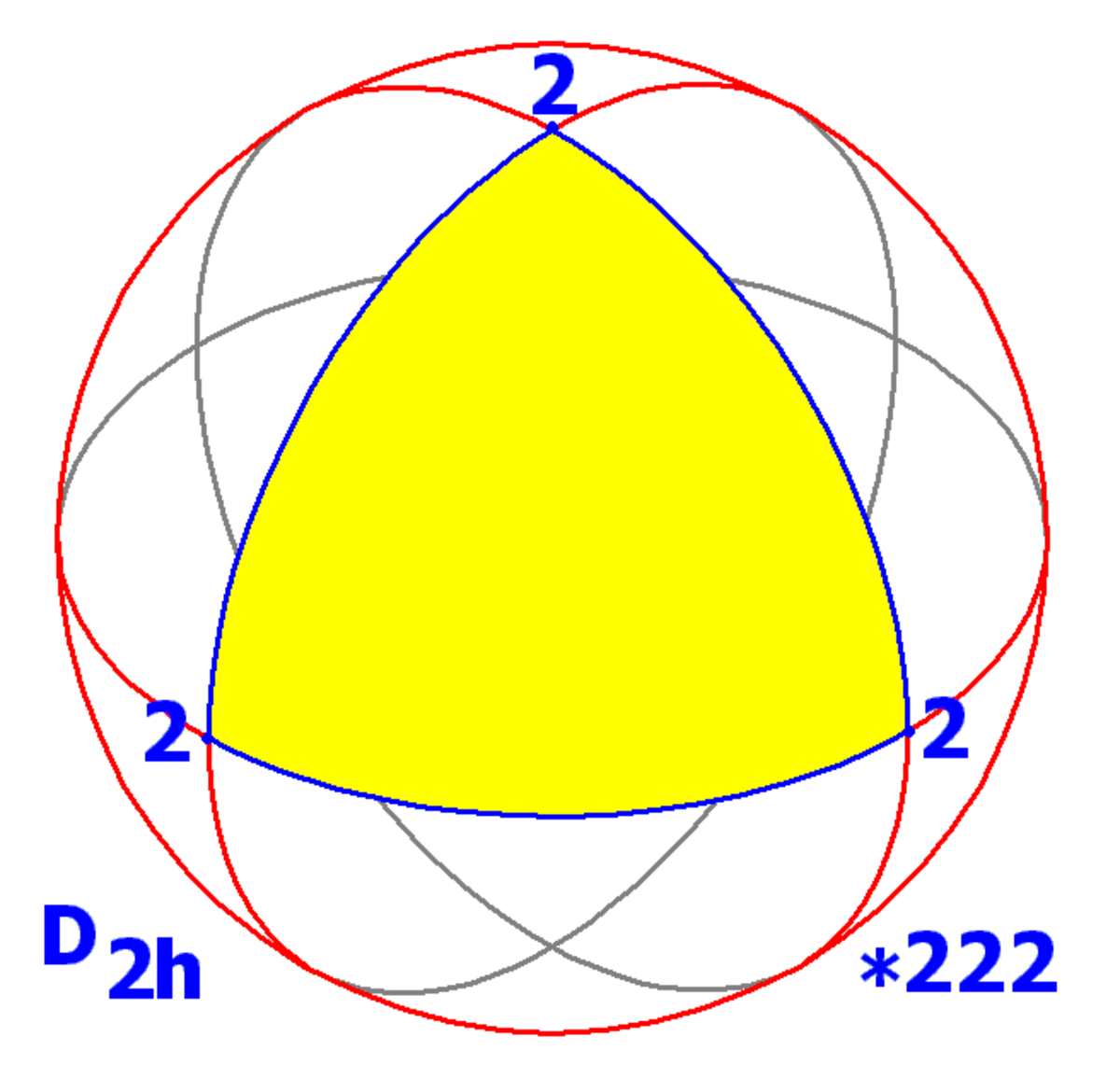
(2 2 2) |
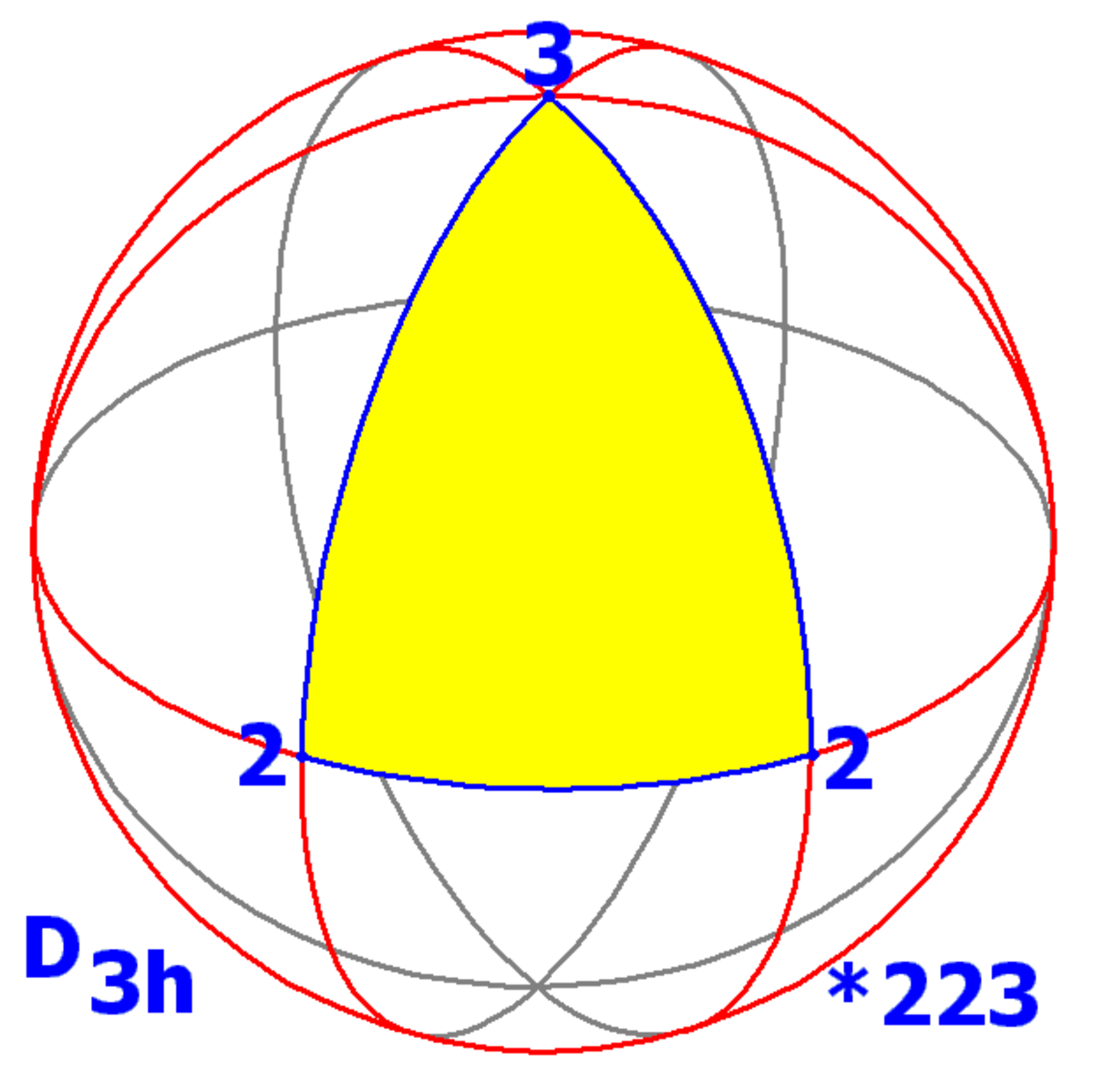
(3 2 2) | 100px ( 3 3 2) | 100px (4 3 2) | 100px (5 3 2) |
Les groupes de symétrie ci-dessus incluent seulement les solutions entières sur la sphère. La liste des triangles de Schwarz incluent des nombres rationnels, et déterminent l'ensemble entier de solutions des polyèdres uniformes.
| Plan euclidien | Hyperbolique | ||
|---|---|---|---|
| p4m | p3m | p6m | |
| *442 | *333 | *632 | *732 |
| 100px (4 4 2) |

(3 3 3) |

(6 3 2) |

(7 3 2) |
Dans les pavages ci-dessus, chaque triangle est un domaine fondamental, coloré par réflexions paires et impaires.