Diagramme de Coxeter-Dynkin - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
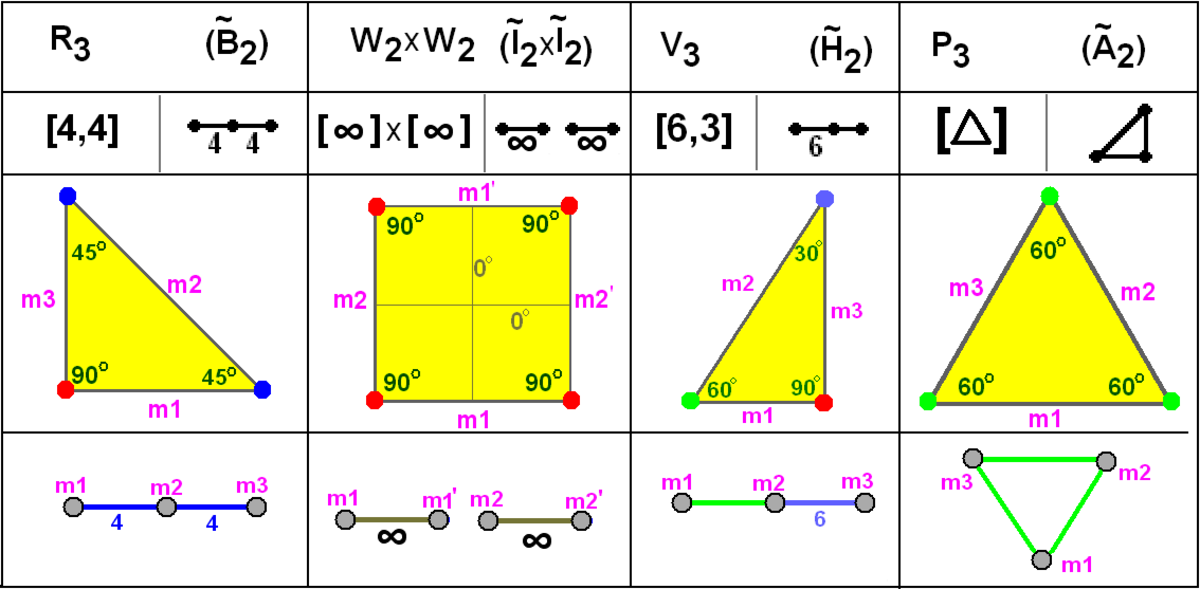
En géométrie, un diagramme de Coxeter-Dynkin est un graphe représentant un ensemble relationnel de miroir (ou d'hyperplans de réflexion) dans l'espace pour une construction kaléidoscopique.
En tant que graphe lui-même, le diagramme représente les groupes de Coxeter, chaque nœud du graphe représente un miroir (facette du domaine) et chaque branche du graphe représente l'ordre de l'angle diédrique entre deux miroirs (sur une arête du domaine).
En plus, les graphes ont des anneaux (cercles) autour des nœuds pour les miroirs actifs représentant un polytope uniforme précis.
Le diagramme est issu du diagramme de Dynkin.
Description
Le diagramme peut aussi représenter les polytopes en ajoutant des anneaux (cercles) autour des noeuds. Chaque diagramme doit avoir au moins un nœud actif pour représenter un polytope.
Les anneaux expriment une information : si un point générateur est dans ou en dehors du miroir. Plus précisément, un miroir est actif (il crée des réflexions) seulement lorsque des points sont en dehors du miroir, donc ajouter un anneau signifie qu'un point est en dehors du miroir et créé une réflexion.
Les arêtes sont étiquetées avec un entier n (ou quelquefois plus généralement un nombre rationnel p/q) représentant un angle diédrique de 180/n. Si une arête n'est pas étiquetée, elle est supposée être 3. Si n=2, l'angle est 90 degrés et les miroirs n'ont pas d'interaction, et l'arête peut être omise. Deux miroirs parallèles peuvent être marqués avec "∞".
En principe, n miroirs peuvent être représentés par un graphe complet dans lequel toutes les n*(n-1)/2 sont dessinées. En pratique, les configurations intéressantes de miroirs incluront un nombre d'angles droits, et les arêtes correspondantes peuvent être omises.
Les polytopes et les pavages peuvent être engendrés en utilisant ces miroirs et un point générateur unique. Les images miroir créent des nouveaux points comme réflexions. Les arêtes peuvent être créées entre les points et une image miroir. Les faces peuvent être construites par cycles d'arêtes créées, etc.
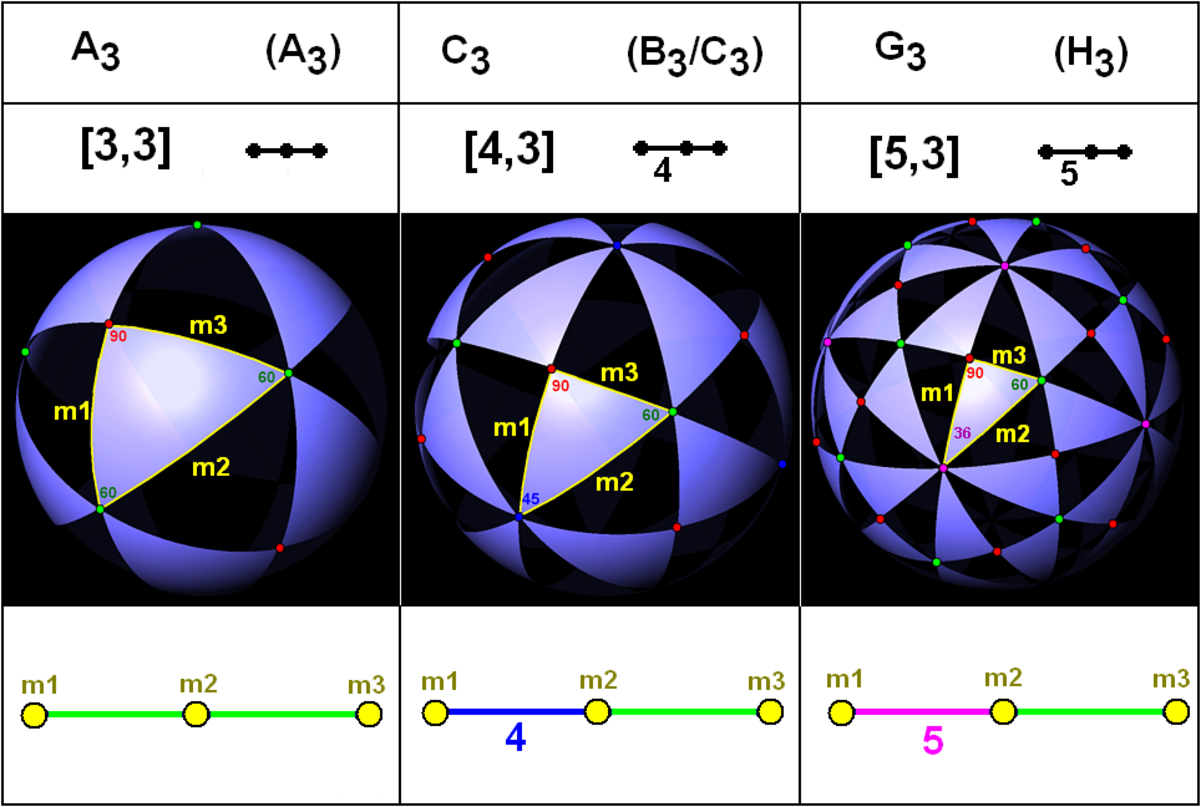
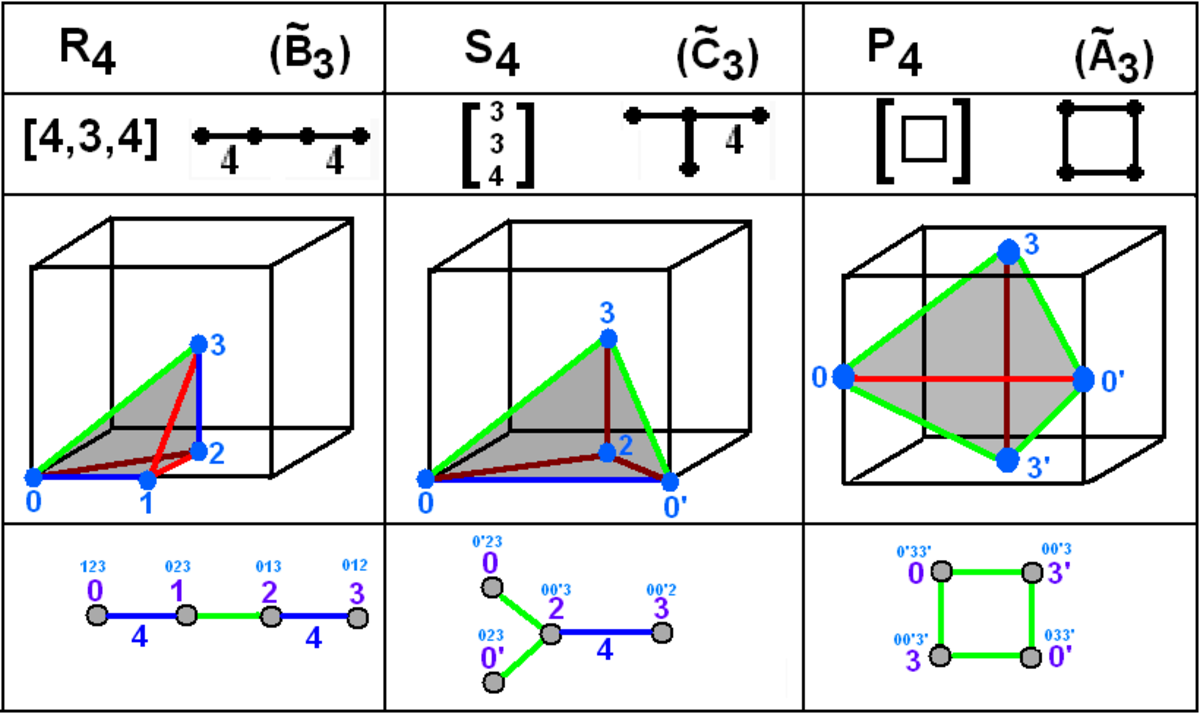
Groupes finis de Coxeter
Les familles de polytopes convexes uniformes sont définis par les groupes de Coxeter.
Notes :
- Trois symboles différents sont donnés pour les mêmes groupes - une lettre/nombre, un ensemble de nombres avec des accolades et le diagramme de Coxeter.
- Les groupes bifurqués Bn sont aussi donnés par la notation h[] représentant le fait que c'est une version demie ou alternée des groupes réguliers Cn.
- Les groupes bifurqués Bn et En sont aussi étiquetés par un exposant [3a,b,c] où a,b,c sont le nombre de segments dans chacune des 3 branches.
| n | A1+ | B4+ | C2+ | D2p | E6-8 | F4 | G2-4 |
|---|---|---|---|---|---|---|---|
| 1 | A1=[] | ||||||
| 2 | A2=[3] | C2=[4] | D2p=[p]
| G2=[5] | |||
| 3 | A3=[3²]
| B3=A3=[30,1,1]
| C3=[4,3] | G3=[5,3] | |||
| 4 | A4=[3³]
| B4=h[4,3,3]=[31,1,1]
| C4=[4,3²]
| E4=A4=[30,2,1]
| F4=[3,4,3] | G4=[5,3,3] | |
| 5 | A5=[34]
| B5=h[4,3³]=[32,1,1]
| C5=[4,3³]
| E5=B5=[31,2,1]
| |||
| 6 | A6=[35]
| B6=h[4,34]=[33,1,1]
| C6=[4,34]
| E6=[32,2,1]
| |||
| 7 | A7=[36]
| B7=h[4,35]=[34,1,1]
| C7=[4,35]
| E7=[33,2,1]
| |||
| 8 | A8=[37]
| B8=h[4,36]=[35,1,1]
| C8=[4,36]
| E8=[34,2,1]
| |||
| 9 | A9=[38]
| B9=h[4,37]=[36,1,1]
| C9=[4,37]
| ||||
| 10+ | .. | .. | .. |
Note : (les noms alternatifs comme les groupes simples de Lie sont donnés)
- An forme la famille du polytope simplex. (de même que An)
- Bn est la famille des polytopes de demi-mesure, commençant à n=4 avec le 24-cellules et n=5 avec le penteract. (aussi nommé Dn)
- Cn forme la famille des hypercubes. (de même que Cn)
- D2n forme les polygones réguliers. (aussi nommé I1n)
- E6,E7,E8 sont les générateurs des polytopes semi-réguliers de Gosset (de même que E6,E7,E8)
- F4 est la famille du polychore 24-cellules. (de même que F4)
- G3 est la famille du polyèdre dodécaèdre/icosaèdre. (aussi nommé H3)
- G4 est la famille du polychore 120-cellules/600-cellules. (aussi nommé H4)