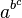Ordre des opérations - Définition

Introduction

En mathématiques, la priorité des opérations ou ordre des opérations précise l'ordre dans lequel les calculs doivent être effectués dans une expression complexe. Les priorités opératoires ainsi que les propriétés d'associativité permettent de limiter l'usage des parenthèses qui précisent normalement les calculs à effectuer en premier.

Les types d’opération par ordre descendant de priorité sont :

1. les parenthèses ;
2. les exposants ;
3. les multiplications et divisions ;
4. les additions et soustractions.

Ainsi un calcul comme 7 + 2 × 6 ,

• doit se lire 7 + (2 × 6) = 7 + 12 = 19
• et ne se lit pas (7 + 2) × 6 = 9 × 6 = 54 comme on serait tenté de le faire par lecture de gauche à droite.

Une calculatrice scientifique prend en compte cet ordre des opérations.

De l'écriture avec parenthèses à l'écriture sans parenthèse

En mathématiques, les opérations de base, addition, soustraction, multiplication, division, exponentiation sont binaires, c'est-à-dire, qu'à deux éléments, on associe un troisième appelé résultat de l'opération. Dans une expression complexe, il est normalement nécessaire de retrouver ces associations par paires. Les parenthèses permettent de déterminer avec précision les paires concernées. Ainsi une écriture sous la forme a+b.c-d+e ne permet pas d'identifier les paires concernées et peut être l'écriture incomplète de

((a+b).(c-d))+e = (A.B) + e avec A = a+b et B=c-d

Les parenthèses définissent un ordre de calcul consistant à calculer d'abord les parenthèses les plus intérieures.

Mais l'expression incomplète pourrait tout autant être celle de

((((a+b).c))-d) + a (si on prenait comme convention l'ordre de lecture)

(a + (b.c))-(d+a)

((a+(b.c))-b) + a

(a+((b.c)-b))+b

ou autres

Entre la présence complète de toutes les parenthèses et l'écriture ambiguë sans aucune parenthèse, il a fallu définir certaines règles.

Associativité

Les premières sont héritées des propriétés d'associativité des lois utilisées. C'est le cas de l'addition et de la multiplication.

Ainsi les calculs de

(a.b).c

et

a.(b.c)

donnant le même résultat, on autorise la suppression des parenthèses, le calcul

a.b.c= (a.b).c=a.(b.c)

pouvant s'effectuer dans l'ordre de son choix. Il en est de même de l'écriture a + b + c qui s'effectue dans l'ordre de son choix.

Il n'en est pas de même pour des mélanges d'additions et de soustractions. Ainsi les calculs de

(a - b) + c

et de

a - (b+c)

ne donnent pas le même résultat. La convention, là, est de voir dans une soustraction l'addition de l'opposé. Une écriture comme a - b + c est alors une abréviation autorisée de a + (-b) + c.

Une telle convention n'est pas aussi explicite pour des mélanges de divisions et de multiplications. Les calculs de

(a:b).c

et de

a:(b.c)

ne donnent pas le même résultat. L'idée de considérer l'expression a:b.c comme (a:b).c n'est pas universellement reconnue. Ainsi encore certaines calculatrices, effectuent le calcul de

3:2a comme 3/(2a)

et effectuent le calcul

3:2* 2 comme (3:2)*2.

L'écriture sous forme fractionnaire, présentant un délimitant fractionnaire, évite toute ambiguïté de ce genre et limite l'usage de la parenthèse :

(a:b).c s'écrit alors ,

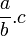
et l'écriture a:(bc),

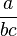
Le cas de la puissance, à cause de sa disposition spatiale, pose un problème légèrement différent : le calcul de (a^b)^c n'a pas même valeur que a^(b^c). La présence d'un délimitant spatial permet en partie de lever l'ambiguïté : l'expression

est une traduction sans parenthèse de la seconde expression. La première expression, elle, nécessite la présence des parenthèses ou bien un début de calcul

(a^b)^c = a^bc

Niveau opératoire

Il existe ensuite des niveaux opératoires qui précisent, en cas d'absence de parenthèses, les calculs à effectuer en premier : il s'agit de calculer d'abord les puissances, ensuite les produits et quotients et enfin les additions et les soustractions. Les parenthèses pouvant être remplacées par des indications de positions comme pour les fractions ou les exposants, ou des barres comme pour les racines.

Ainsi par convention l'écriture de départ,

a + b.c - d + a

ne présente plus aucune ambiguïté avec ces nouvelles conventions et ne peut valoir que le résultat de la somme suivante :

a +(b.c) + (-d) + e.

et une expression comme

2x² - 3x + 5

ne peut se lire que sous la somme suivante

2(x²))+(-3x) + 5

Lorsque le calcul à effectuer ne respecte pas cet ordre d'exécution, les parenthèses sont alors là pour indiquer les priorités non conventionnelles. Ainsi, l'expression

a+b.c+d

étant interprétée comme

a + (bc) + d,

le produit de deux sommes doit comporter les parenthèses

(a + b).(c +d)