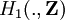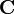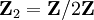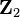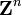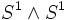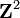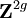Théorème d'Hurewicz - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Exemples
Le théorème d'Hurewicz permet de calculer le premier groupe d'homologie connaissant le groupe fondamental :
| Espace topologique | Description | Groupe fondamental |
|
|---|---|---|---|
| Espace contractile | Tout lacet se contracte en un point. | Groupe trivial | 0 |
| S1 | Le cercle unité de
| Le groupe additif des entiers naturels Z | Z |
| PnR | L'espace projectif réel de dimension n. |
|
|
| Tn | Le tore de dimension n. | Le produit cartésien
|
|
|
| La somme de deux cercles appelée la figure du huit. | Le groupe libre L2. |
|
| Σg | La surface compacte orientée de genre g. | Le groupe présenté par < a1,...,b1,...,bg | [a1,b1]...[ag,bg] = 1 > . |
|