Théorème d'Hurewicz - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En topologie algébrique, le théorème d'Hurewicz est une description du premier groupe d'homologie singulière d'un espace topologique X à l'aide du groupe fondamental de X. Il a été attribué au mathématicien Hurewicz.
Énoncé
Le groupe fondamental d'un espace topologique connexe par arcs X en un point x est défini comme l'ensemble des classes d'homotopie de lacets de X en x, muni de la loi de concaténation des lacets. Il est noté π1(X,x). Si y est un second point de X, les groupes π1(X,x) et π1(X,y) sont isomorphes : des isomorphismes peuvent être construits en utilisant un chemin de x à y. Cependant, de tels isomorphismes sont uniquement définis à conjugaison près.
Si G est un groupe, on note [G,G] le sous-groupe normal de G engendré par les commutateurs de G, appelé groupe dérivé. Le groupe Gab: = G / [G,G] s'appelle l'abélianisé de G. Plus grand quotient abélien de G, il est caractérisé par la propriété universelle suivante :
-
- Tout morphisme de groupe de G dans un groupe abélien se factorise à travers Gab.
Un automorphisme intérieur de G préserve les commutateurs, et induit par passage au quotient l'identité sur l'abélianisé Gab. En particulier, alors que le groupe fondamental de (X,x) dépend du point de base x, son abélianisé est un invariant algébrique de X.
La construction de l'homologie singulière est supposée connue du lecteur. On note
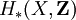
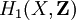
Théorème :
- Soit X un espace topologique connexe par arcs. Un lacet
![f:[0,1]\rightarrow X](https://static.techno-science.net/illustration/Definitions/autres/c/c706d9d5b3ec876a8349e3204ab59ee8_3dc2c80ba3bb609e9750749a84f4e4af.png)
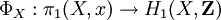
- De plus, si Y est également connexe par arcs, toute application continue
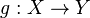
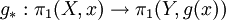
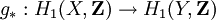
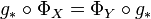
Autrement dit,
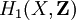
- Le foncteur H1 qui à un "objet" X associe
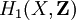
- La foncteur
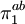
Le théorème d'Hurewicz donne l'existence d'un isomorphisme de foncteurs Φ de
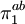
Preuve
Le théorème d'Hurewicz énonce l'existence d'un morphisme de groupes et sa bijectivité. L'injectivité du morphisme d'Hurewicz demande plus de travail que sa surjectivité. La bijectivité sera ici établie en donnant la construction explicite d'un inverse. On note Δ0 le point, Δ1 = [0,1] le 1-simplexe standard, et Δ2 le 2-simplexe standard où les points sont repérées en coordonnées barycentriques par (s,t,u) avec s+t+u=1.
Existence du morphisme d'Hurewicz
Un lacet f de X en un point x est une application continue
![f:[0,1]\rightarrow X](https://static.techno-science.net/illustration/Definitions/autres/c/c706d9d5b3ec876a8349e3204ab59ee8_3dc2c80ba3bb609e9750749a84f4e4af.png)
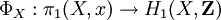
Cette application est un morphisme de groupes : pour deux lacets f et g de X en x,
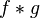
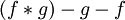
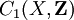
Comme
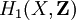
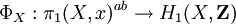
Construction de l'inverse
Comme X est connexe par arcs, pour y un point de X, introduisons un chemin λy d'origine x et d'extrémité y (l'axiome du choix est ici utilisé). Pour tout 1-simplexe f de X, on définit :
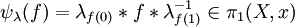
Le lacet ψλ(f) dépend malheureusement du choix des chemins λy : il en va de même de sa classe dans l'abélianisé du groupe fondamental. L'application ψλ induit une application Z-linéaire :
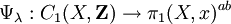
Des arguments techniques (détaillés ci-dessous) montrent les résultats remarquables suivants :
- Le noyau de Ψλ contient les 1-bords (bords de 2-simplexes).
- Malgré la dépendance déjà soulignée en les choix des chemins utilisés, l'application ΨΛ en restriction aux 1-cycles en est indépendante.
De fait, Ψλ induit par restriction et passage au quotient un morphisme Ψ indépendant de λ :
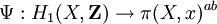
Ce morphisme Ψ a été construit pour être l'inverse du morphisme d'Hurewicz Φ = ΦX :
- Pour un élément α de π1(X,x)ab, représenté par un lacet f de X en x, l'image ΦX(f) est représentée par f, vu comme un 1-cycle. Par définition, ΨΦ(α) est la classe de
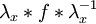
- Pour tout 1-simplexe f,
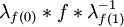
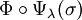
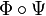
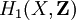
- Soit
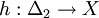
- f0(s) = h(0,s,1 − s) ;
- f1(s) = h(s,0,1 − s) ;
- f2(s) = h(s,1 − s,0).
- Le bord de h est précisément f0 − f1 + f2. Or, un calcul donne :
-
- où on a utilisé f0(1) = f2(0), f2(1) = f1(1), et f1(0) = f0(1). Comme
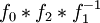
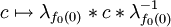
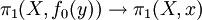
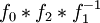
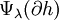
-
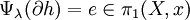
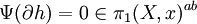
En effet, si μ est un autre choix de chemins d'origine x, et si
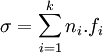
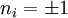

![\Psi_{\lambda}(\partial h)=\left[\lambda_{f_0(0)}*f_0*\lambda_{f_0(1)}^{-1}\right]-\left[\lambda_{f_1(0)}*f_1*\lambda_{f_1(1)}^{-1}\right] +\left[\lambda_{f_2(0)}*f_2*\lambda_{f_2(1)}^{-1}\right]](https://static.techno-science.net/illustration/Definitions/autres/e/eab437e2bdfba38452f5c91caf016e78_128a388ba5892dcdbc712ad1c18ac831.png)
![=\left[\lambda_{f_0(0)}*f_0*\lambda_{f_0(1)}^{-1}\right]+\left[\lambda_{f_2(0)}*f_2*\lambda_{f_2(1)}^{-1}\right] +\left[\lambda_{f_1(1)}*f_1^{-1}*\lambda_{f_1(0)}^{-1}\right]](https://static.techno-science.net/illustration/Definitions/autres/6/6236ce256753fc4c96a21f760b55e37a_555c8723d79f2f6668748513702767f9.png)
![=\left[\lambda_{f_0(0)}*f_0*f_2*f_1^{-1}*\lambda_{f_0(0)}^{-1}\right]](https://static.techno-science.net/illustration/Definitions/autres/e/e7c2ad1a5c5b10378a539c20814799cf_c0cfa4236c744936fa1a32f13eaea952.png)
![\Psi_{\mu}\left[\sum_{i=1}^kn_i.f_i\right]=\sum_{i=1}^kn_i.\left[\mu_{f_i(0)}*f_i*\mu_{f_i(1)}^{-1}\right]](https://static.techno-science.net/illustration/Definitions/autres/4/4e69ca880acac32f556f547fe74f5c3e_29e14214316b178d5d78fbc7076174f0.png)
![=\sum_{i=1}^kn_i.\left(\left[\mu_{f_i(0)}*\lambda_{f_i(0)}^{-1}\right] + \left[\lambda_{f_i(0)}f_i*\lambda_{f_i(1)}^{-1}\right]+\left[\lambda_{f_i(1)}^{-1}\mu_{f_i(1)}^{-1}\right]\right)](https://static.techno-science.net/illustration/Definitions/autres/9/9cff16d1b79990b528db040228add7af_04d1903fa6a9732d1454c1431bd8c756.png)
![=\sum_{i=1}^kn_i.\left[\mu_{f_i(0)}*\lambda_{f_i(0)}^{-1}\right]-\sum_{i=1}^k \left[\mu_{f_i(1)}*\lambda_{f_i(1)}^{-1}\right]+\Psi_{\lambda}\left[\sum_{i=1}^kn_i.f\right]](https://static.techno-science.net/illustration/Definitions/autres/2/29beee4d5a94218962f16e4dadb4db23_372ccea55f821abbd54e387932ca65b9.png)
![=\Psi_{\lambda}\left[\sum_{i=1}^kn_i.f\right]](https://static.techno-science.net/illustration/Definitions/autres/a/a2f4ad8a136c30f613c3afb3c67e49b5_3c853ed9b09cbbf5d0d96d80453e0af7.png)

















































