Cercle unité - Définition

Introduction

Le cercle unité est une expression courante pour désigner l'ensemble des nombres complexes de module 1. Si le module est vu comme une norme euclidienne, le cercle est une courbe de longueur 2π, et est le bord d'un disque d'aire π. Le cercle unité est l'image de l'axe des imaginaires purs iR par l'exponentielle complexe.

Le cercle unité est stable par produit. C'est un sous-groupe du groupe des inversibles. C'est le sous-groupe compact maximal de C^*.

Cercle unité et trigonométrie

Éléments d'histoire

D'après le site Earliest Known Uses of Some of the Words of Mathematics, l'expression “unit circle” est attribuée à George Albert Wentworth vers 1890. L'expression fut utilisée pour décrire le cercle trigonométrique, et introduire les fonctions trigonométriques, tel qu'elles sont enseignées aujourd'hui dans l'enseignement des mathématiques dans le secondaire.

Cercle unité comme bord du plan hyperbolique

La lecture de cette partie nécessite quelques connaissances en géométrie riemannienne.

Le plan hyperbolique est le disque unité D muni de la métrique riemannienne

.

En bleu, les géodésiques issues d'un point à l'infini.
En rouge, les horosphères centrées en ce point.

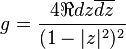
Cette métrique est conforme à la métrique euclidienne : deux courbes qui s'intersectent transversalement forment le même angle. Mais la distance est modifiée, et en particulier, pour atteindre un complexe de module 1, il faut parcourir une longueur infinie. Le cercle unité U est regardé comme l'ensemble des points à l'infini du plan hyperbolique D. Il est en général noté . Le plan hyperbolique est une variété riemmanienne de dimension 2 dont la courbure est constante égale à -1. D'autres présentations sont possibles et sont données dans l'article géométrie hyperbolique.

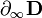
Par définition, les géodésiques de D sont les courbes qui minimisent au moins localement la distance. Ce sont exactement les diamètres de D ou les arcs de cercles orthogonaux au cercle unité. Il est remarquable que ces courbes minimisent globalement la distance. Autrement dit, pour tous complexes z et w de modules <1, il existe un unique géodésique passant par z et w. Chaque géodésique détermine deux points à l'infini (deux points sur le cercle), et réciproquement, deux points distincts à l'infini définissnt une unique géodésique. Par exemple, deux points diamètralement opposés z et -z sur le cercle unité correspondent au diamètre (-z,z). Pour résumer, si z et w sont deux nombres complexes distincts de module (qu'ils soient à l'intérieur du disque unité D ou sur le bord à l'infini ), alors il existe une unique géodésique C_z,w contenant z et w, et qui dépend continument de z et w.

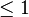
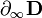
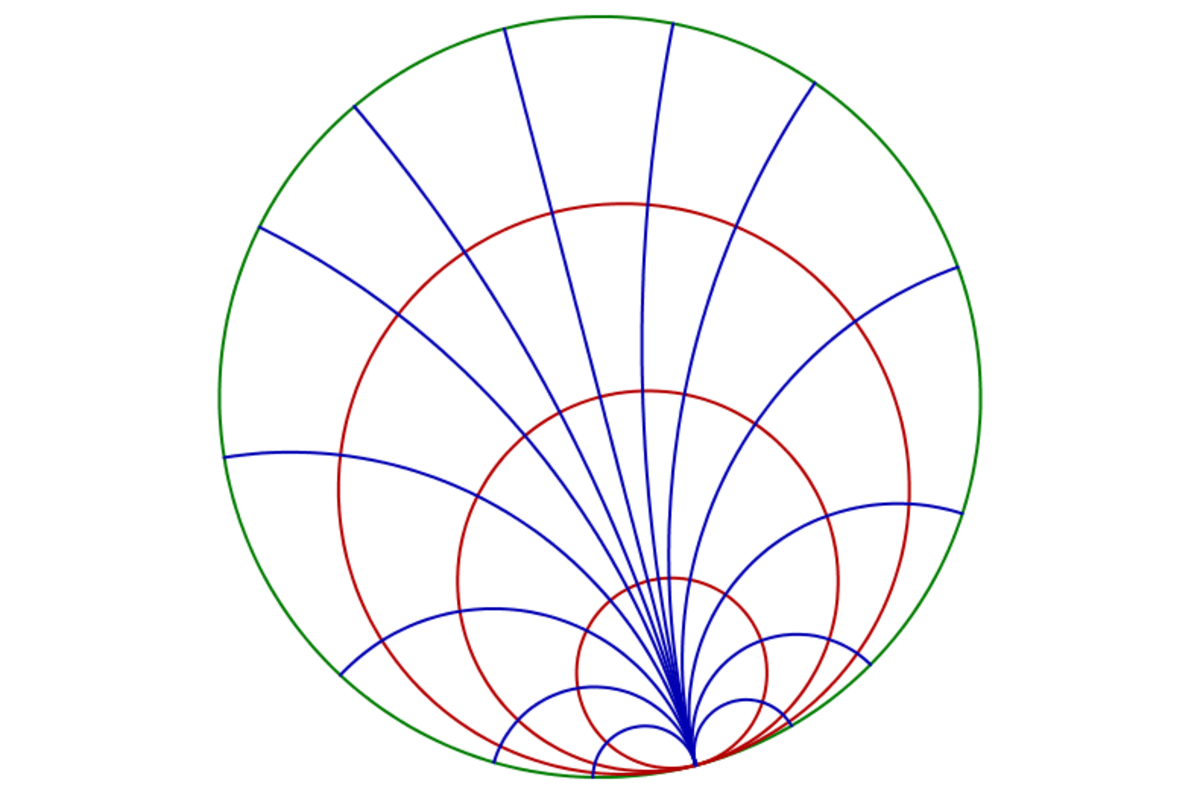
Si z est un nombre complexe de module 1, les géodésiques ayant z pour point à l'infini forment un feuilletage de D. Les cercles intérieurs à D et tangents à U en z sont appelés les horosphères de centre z. Elles intersectent orthogonalement les géodésiques issues de z.

Ces propriétés se généralisent pour les variétés de Hadamard pour lesquelles on définit une sphère à l'infini dont les points paramètrent les géodésiques. Il s'agit d'une compactification géométrique en courbure négative, et on renvoie le lecteur à l'article variété de Hadamard.

Références