Tore - Définition

Introduction

Tore

Un tore est un solide géométrique représentant un tube courbé refermé sur lui-même. Le terme « tore » comporte différentes acceptions plus spécifiques selon le contexte :

• En ingénierie ou en géométrie élémentaire, un tore désigne un solide de révolution de l'espace obtenu à partir d'un cercle, ou bien sa surface. Une chambre à air, une bouée, certains joints toriques d'étanchéité ou encore un beignet ("donut" nord-américain) ont ainsi une forme plus ou moins torique.
• En architecture, un tore correspond à une moulure ronde, semi-cylindrique, entourant le pied d'une colonne ou d'un pilier.
• En mathématiques, plus particulièrement en topologie, un tore est un quotient d'un espace vectoriel réel de dimension finie par un réseau, ou tout espace topologique qui lui est homéomorphe. La surface du solide de révolution décrit ci-dessus est généralement homéomorphe à (R/Z)×(R/Z), exception faite des cas de dégénérescence.

Le solide de révolution

Un tore est engendré par la rotation d'un cercle autour d'un autre cercle.

Le tore est également obtenu par recollement des côtés opposés d'un carré

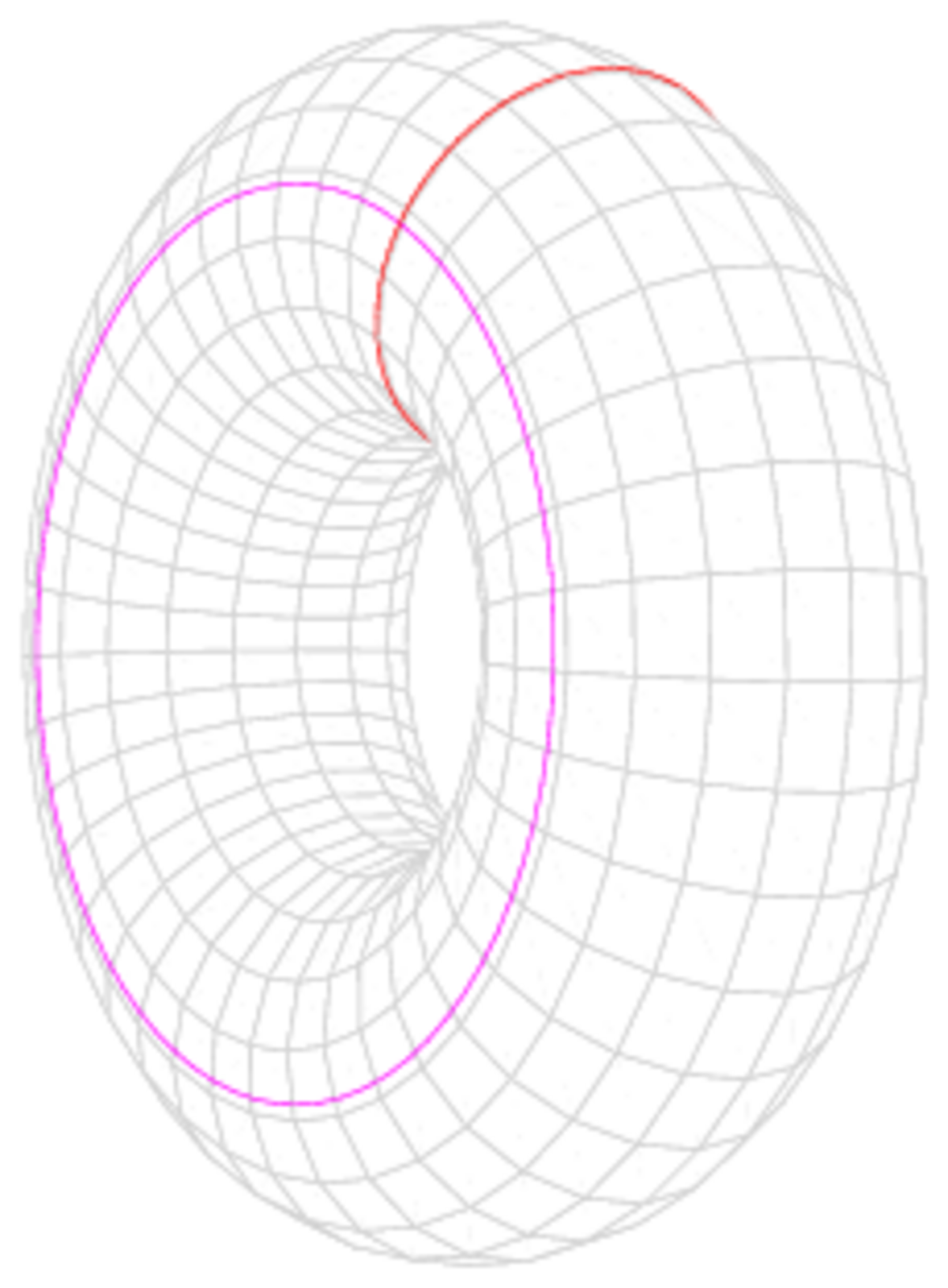
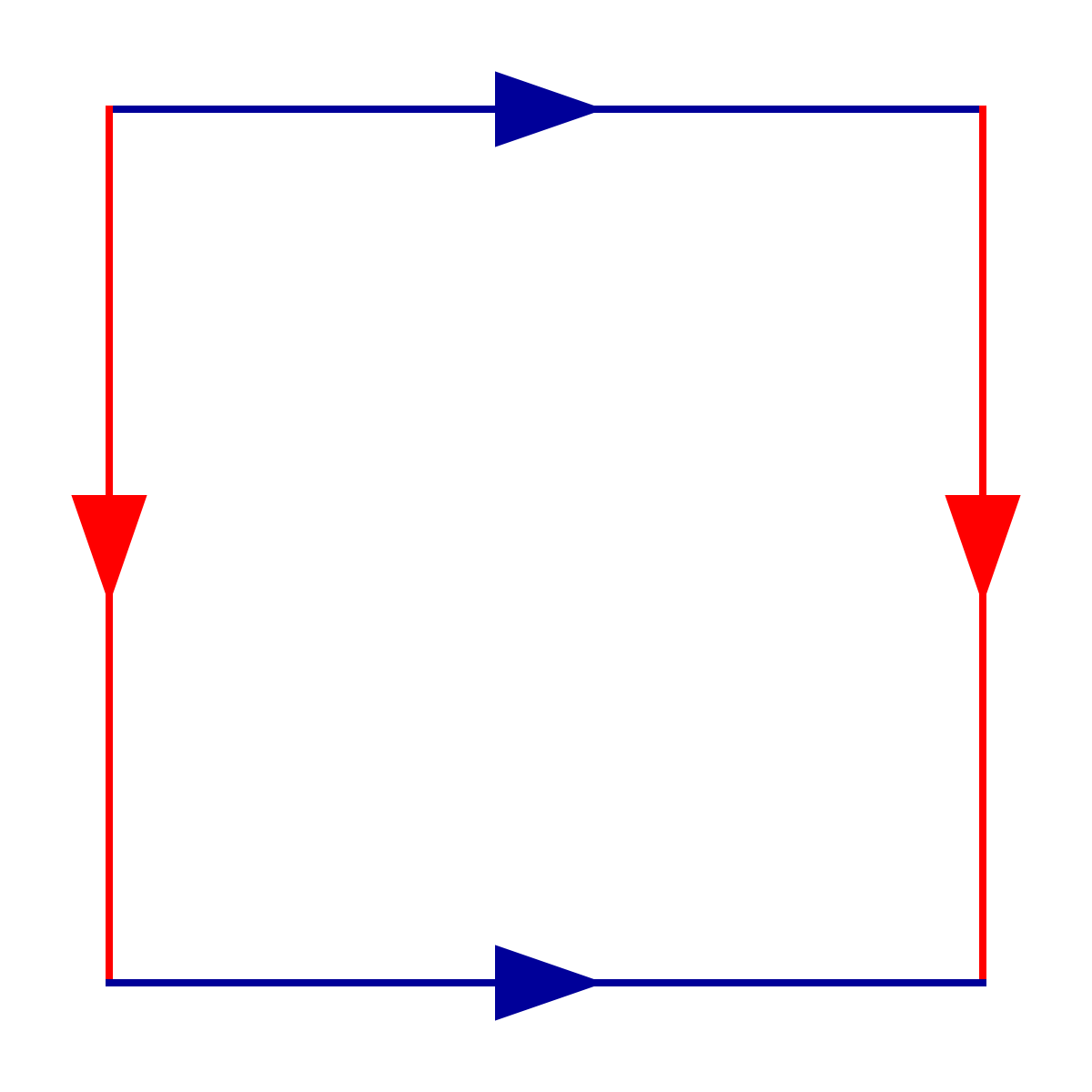
Un tore désigne le volume de l'espace euclidien R³ engendré par la rotation d'un cercle C de rayon r autour d'une droite affine D située dans son plan à une distance R de son centre. Dans cette acception, certains auteurs désignent par tore plein le solide obtenu, réservant le terme tore pour la surface correspondante. À l'action d'une isométrie affine directe près, le tore (plein) est uniquement déterminé par les deux paramètres réels R et r.

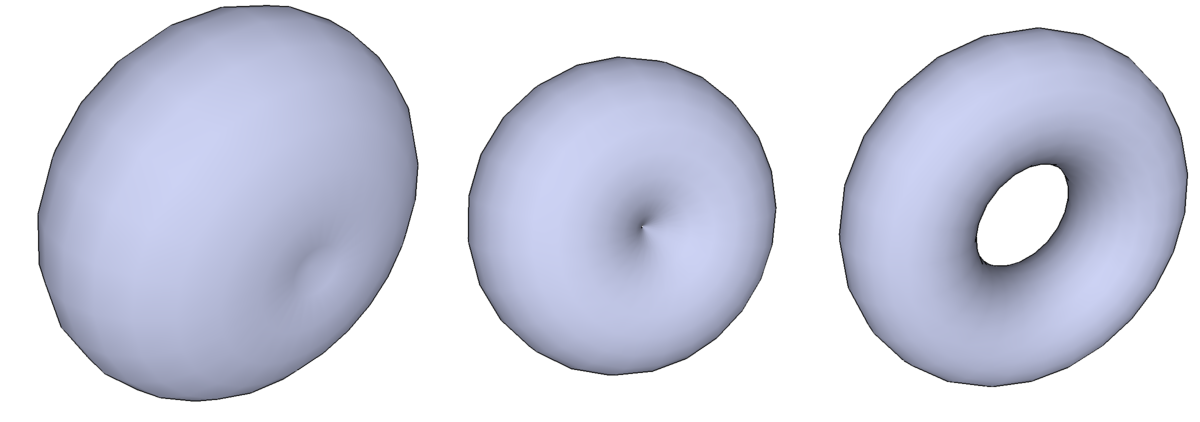
La forme du tore (plein) dépend du signe de R-r :

• Pour R = 0, alors le tore (plein) correspondant est une boule (solide obtenu par la rotation d'un disque autour de l'un de ses diamètres). Certains auteurs réservent la dénomination tore pour R-r positif, voire strictement positif.
• Si R < r, le tore est dit « croisé » et ressemble visuellement à une citrouille ; le solide est topologiquement une boule fermée de l'espace tridimensionnel, et sa surface une sphère.
• Si R = r, le tore est dit « à collier nul ».
• si R > r, le tore est dit « ouvert » et ressemble à une chambre à air (exemple francophone) ou à un donut (exemple anglophone).

Aire et volume

Pour R-r positif ou nul, on a :

• Aire du tore : A = 4 π² r R ;
• Volume intérieur du tore : V = 2 π² r² R.

Les théorèmes de Guldin permettent d'obtenir ces résultats, et aussi de déterminer les formules de l'aire et du volume du tore croisé (pour R<r).

Groupe des isométries

Pour R>0, parmi les isométries remarquables du tore, on distingue :

• Les rotations r_u d'axe (supposé orienté) D et d'angle u ;
• Le retournement a par rapport au plan affine P orthogonal à D passant par le centre de C ;
• Le retournement b_Q par rapport à tout plan affine Q contenant D ;
• La symétrie centrale s par rapport au projeté orthogonal O de C sur D ;
• Les symétries axiales par rapport à toute droite passant par O et contenue dans P ;
• Les composées d'une rotation r_u par le retournement a.

Evidemment, la symétrie centrale et les symétries axiales s'obtiennent comme composées des retournements décrits. Le groupe G des isométries du tore est isomorphe au produit direct de Z/2Z par le produit semi-direct de S¹ par Z/2Z :

.

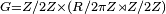
Un isomorphe naturel est décrit comme suit :

• r_u correspond à (0,u,0) ;
• a correspond à (1,0,0) ;
• Pour un plan Q fixé arbitraire, b_Q correspond à (0,0,1).

En particulier, b_ru(Q)=r_ub_Qr_-u correspond à (0,u,1) ; s correspond à (1,π,0) ; ...

Colorier un tore

Le théorème des quatre couleurs ne s'applique pas pour un tore : il est possible de diviser la surface d'un tore en 7 zones de couleurs différentes (maximum) de sorte que chacune touche toutes les autres.

Applications

• En recherche nucléaire pour la production d'énergie par fusion, dans les réacteurs de type tokamak, le plasma est contenu par de forts champs magnétiques dans une chambre de forme torique. L'un de ces réacteurs porte d'ailleurs le nom de Tore Supra. C'est aussi la forme des chambres à vide des accélérateurs de particules du type synchrotron (en négligeant les canaux d'entrée et de sortie).
• En électricité, la forme idéale du bobinage d'un transformateur est celle du tore.