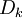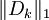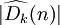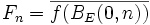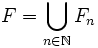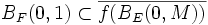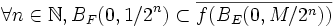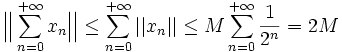Théorème de Banach-Schauder - Définition

Démonstration

Pour montrer que f est ouverte, il suffit par linéarité de montrer que l'image de tout voisinage de 0 (dans E) par f est un voisinage de 0 (dans F), i.e

(Par homogénéité de f, il suffit même de le faire pour un seul ). On introduit les fermés suivants :

Comme f est surjective, on dispose de l'égalite ensembliste :

F est un espace de Banach, en particulier il vérifie la propriété de Baire, donc un de ces fermés, F_N est d'intérieur non vide : il contient une boule B_F(y,η).

Le fermé F_2N contient donc la boule B_F(0,η). Par homogénéité de f on dispose ainsi d'un entier M tel que :

Il ne reste plus qu'à faire sauter la barre. Par homogénéité de f, on déduit de ce résultat que :

Montrons que . Pour cela, donnons-nous un

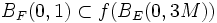
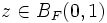
• Il existe x₀ de norme inférieure à M tel que z₁ = z − f(x₀) soit de norme inférieure à 1/2.
• Il existe x₁ de norme inférieure à M / 2 tel que z₂ = z₁ − f(x₁) soit de norme inférieur à 1/4.

On construit par récurrence une suite (x_n) de points de E telle que et soit de norme inférieure à 1 / 2ⁿ.

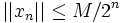
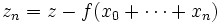
La série est absolument convergente, donc comme E est un espace de Banach, elle converge. De plus,

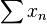
Et, par passage à la limite :

C'est ce qu'il fallait démontrer.

Exemple d'application

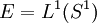
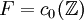
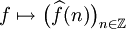
Soient l'espace de Banach des fonctions intégrables sur le cercle, et l'espace des suites complexes indexées par les entiers relatifs et tendant vers zéro. L'application qui associe à la fonction f la suite de ses coefficients de Fourier est continue et injective de E dans F, mais n'est pas surjective. En effet, si tel était le cas, il existerait une constante telle que, pour toute fonction ,

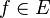
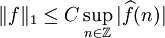
En appliquant une telle inégalité à la suite des noyaux de Dirichlet , on arrive à une contradiction. En effet, est d'ordre log(k) alors que les sont bornés par 1.