Théorème de Banach-Schauder - Définition

Introduction

En analyse fonctionnelle, le théorème de Banach-Schauder, également appelé théorème de l'application ouverte est un résultat fondamental qui affirme qu'une application linéaire continue surjective entre deux espaces vectoriels normés complets est ouverte. C'est une conséquence importante du théorème de Baire, qui affirme que dans un espace métrique complet (et donc en particulier dans un espace de Banach), toute intersection dénombrable d'ouverts denses est dense, ce qui permet de généraliser le théorème de Banach-Schauder aux espaces de Fréchet.

Énoncé

Soient E et F deux espaces de Banach et f une application linéaire continue de E vers F.

Si f est surjective, alors f est ouverte, i.e. l'image de tout ouvert de E par f est un ouvert de F.

Conséquences

Théorème d'isomorphie de Banach

Le théorème de Banach-Schauder a une conséquence fondamentale (en fait, il s'agit d'une forme équivalente du théorème, et non d'un résultat plus faible), appelée théorème d'isomorphie de Banach, théorème de Baire-Banach ou plus simplement théorème de Banach :

Si f est une application linéaire bijective continue entre deux espaces de Banach, alors f est un homéomorphisme.

Théorème du graphe fermé

Le théorème de Banach-Schauder est également à l'origine d'un puissant critère de continuité des applications linéaires entre deux espaces de Banach, il s'agit du théorème du graphe fermé :

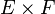
Soit E et F deux espaces de Banach, et f une application linéaire de E dans F. f est continue si et seulement si son graphe est une partie fermée de .

Supplémentaire topologique

Dans le cas de la dimension infinie, rien ne garantit que les projecteurs associés à des sous-espaces supplémentaires soient continus. C'est la raison d'être de la définition suivante :

• Soient E un espace de Banach et F un sous-espace fermé de E. Un sous-espace G est un supplémentaire topologique si et seulement s'il est un supplémentaire algébrique et s'il est fermé.

Un supplémentaire algébrique, par définition est un sous-espace tel qu'il existe une et une unique manière d'écrire un vecteur de E comme somme d'un vecteur de F et d'un vecteur de G.

Le théorème de Banach-Schauder permet de démontrer la proposition suivante :

• Les projecteurs associés à des supplémentaires topologiques sont continus.

Ce résultat est la conséquence de la proposition suivante, utilisée par exemple pour démontrer des propriétés d'orthogonalités dans un espace de Banach.

• Soient E un espace de Banach, F₁ et F₂ deux sous-espaces vectoriels fermés tel que leurs somme soit fermée. Alors il existe une constante C strictement positive tel que tout x de E admette une décomposition de la forme x = x₁ + x₂ avec x₁ élément de F₁, x₂ élément de F₂ et :

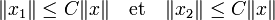
La proposition précédente admet le corollaire suivant :

• Avec les mêmes notations que la proposition précédente, il existe une constante C strictement positive telle que la distance d entre un élément x de E et l'intersection de F₁ et F₂ soit donnée par la formule suivante :

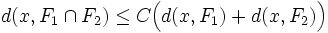
Ce corollaire est aussi utilisé pour établir des propriétés d'orthogonalités.

• Soient E un espace de Banach, F₁ et F₂ deux sous-espaces vectoriels fermés tel que leurs somme soit fermée. Alors il existe une constante C strictement positive tel que tout x de E admette une décomposition de la forme x = x₁ + x₂ avec x₁ élément de F₁, x₂ élément de F₂ et :

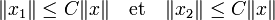
Soit l'espace F₁xF₂ muni de la norme suivante :

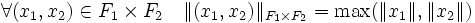
L'espace F₁xF₂ est un Banach et l'application de F₁xF₂ dans E qui à un couple associe la somme des deux éléments est linéaire surjective. L'inégalité triangulaire montre que l'application est continue. Soit x le vecteur de la proposition. Le théorème de Banach-Schauder montre l'existence d'un réel c strictement positif tel que :

Il suffit alors de choisir C comme l'inverse de c.

• Les projecteurs associés à des supplémentaires topologiques sont continus :

C'est un corollaire immédiat de la proposition précédente.

• il existe une constante D strictement positive telle que la distance d entre un élément x de E et l'intersection de F₁ et F₂ soit donnée par la formule suivante :

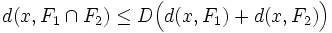
Soit ε un réel strictement positif et C la constante strictement positive établie dans la proposition précédente. Par définition de la distance entre un vecteur et un ensemble, il existe un vecteur y₁ (resp. y₂) de F₁ (resp. F₂) tel que :

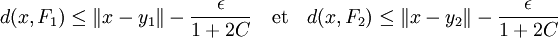
La proposition précédente montre d'un vecteur x₁ (resp. x₂) élément de F₁ (resp. F₂) tel que :

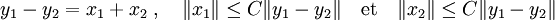
L'égalité suivante montre que x₁ − y₁ est un élément de l'intersection de F₁ et F₂ :

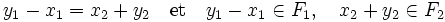
On en déduit :

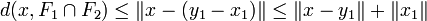
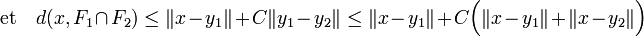
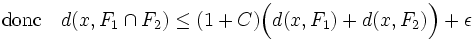
Si D est choisi égal à 1 + C, la majoration précédente est vraie pour tout ε, ce qui démontre la proposition.