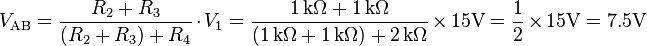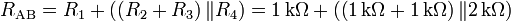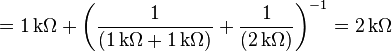Théorème de Thévenin - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l'ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit principalement des propriétés de linéarité et du principe de superposition qui en découle. Il s'utilise pour convertir une partie d'un réseau complexe en un dipôle plus simple.
Énoncé
Un réseau électrique linéaire vu de deux points est équivalent à un générateur de tension parfait dont la force électromotrice est égale à la différence de potentiels à vide entre ces deux points, en série avec une résistance égale à celle que l'on mesure entre les deux points lorsque les générateurs indépendants sont rendus passifs.
La démonstration de ce théorème repose sur le principe de superposition, ce qui permet d'étendre la généralité de son application à tous dispositifs électroniques qui fonctionnent linéairement.
On peut imaginer la situation où l'on relie deux dipôles linéaires désignés respectivement par les lettres A et B, le but de la démarche est alors de trouver un schéma équivalent au dipôle A de sorte que son comportement vis à vis du dipôle B reste identique.
Avant de relier les dipôles A et B, les tensions à vide entre leurs bornes sont respectivement
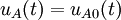
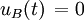
On peut ensuite relier les deux dipôles à l'aide d'un court-cicuit qu'on remplace, toutefois de manière équivalente, par deux sources de tension en série
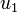
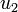
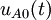
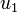
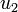
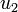
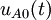
Exemple
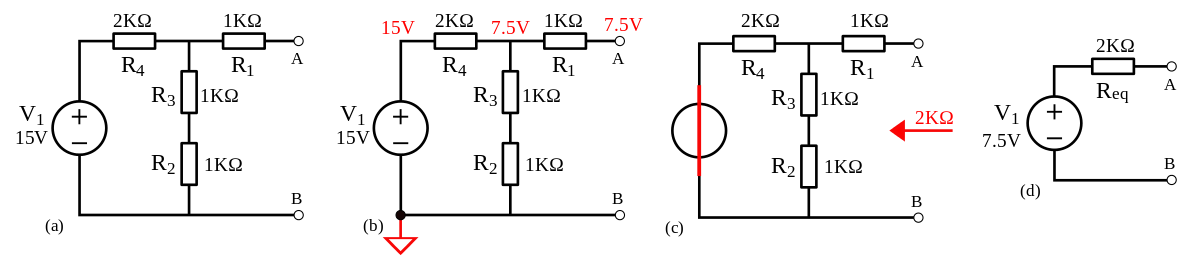
- En (a): Circuit originel.
- En (b): Calcul de la tension aux bornes de AB.
(Notez que R1 n'est pas prise en considération, car les calculs ci-dessus sont faits en circuit ouvert entre A et B, par suite, il n'y a pas de courant qui passe à travers R1 et donc aucune chute de tension n'y apparait)
- En (c): Calcul de la résistance équivalente aux bornes AB en court-circuitant V1.
- En (d): Circuit équivalent de Thévenin. Celui-ci nous permet de trouver aisément le courant dans un dipôle quelconque relié entre les bornes A et B sans qu'on ait à résoudre le circuit au complet.