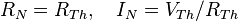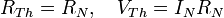Théorème de Thévenin - Définition

Détermination du modèle de Thévenin

Soit un circuit composé de plusieurs sources et de plusieurs résistances possédant deux bornes A et B entre lesquelles est raccordée une charge :

• La tension de Thévenin est la tension calculée ou mesurée, entre les bornes A et B lorsque la charge est déconnectée (tension à vide).
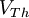
• La résistance de Thévenin est la résistance calculée, ou mesurée, entre les bornes A et B lorsque la charge est déconnectée et que les sources sont éteintes : les sources de tension indépendantes sont remplacées par un court-circuit et les sources de courant indépendantes par un circuit ouvert.

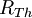
Lorsque la tension de Thévenin est connue, il existe trois autres méthodes pratiques pour mesurer la résistance de Thévenin.

• La première consiste à remplacer la charge par une résistance dont la valeur est connue et à prendre la tension aux bornes de cette résistance. se résout facilement car elle devient alors la seule inconnue de l'équation découlant du théorème du diviseur de tension.
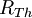
• La deuxième méthode, proche de la première, est celle dite de la demi-tension : on utilise une résistance variable au lieu d'une résistance fixe et on fait varier la valeur de la résistance jusqu'à avoir , les deux résistances sont alors égales.
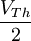
• La dernière méthode fait appel au courant de Norton. Si celui-ci est connu, on utilise la formule suivante: où est le courant calculé ou mesuré, entre les bornes A et B lorsqu'elles sont court-circuitées.

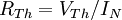
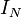
Le théorème de Thévenin s'applique aussi aux réseaux alimentés par des sources alternatives. L'ensemble des résultats est applicable en considérant la notion d'impédance en lieu et place de celle de résistance.

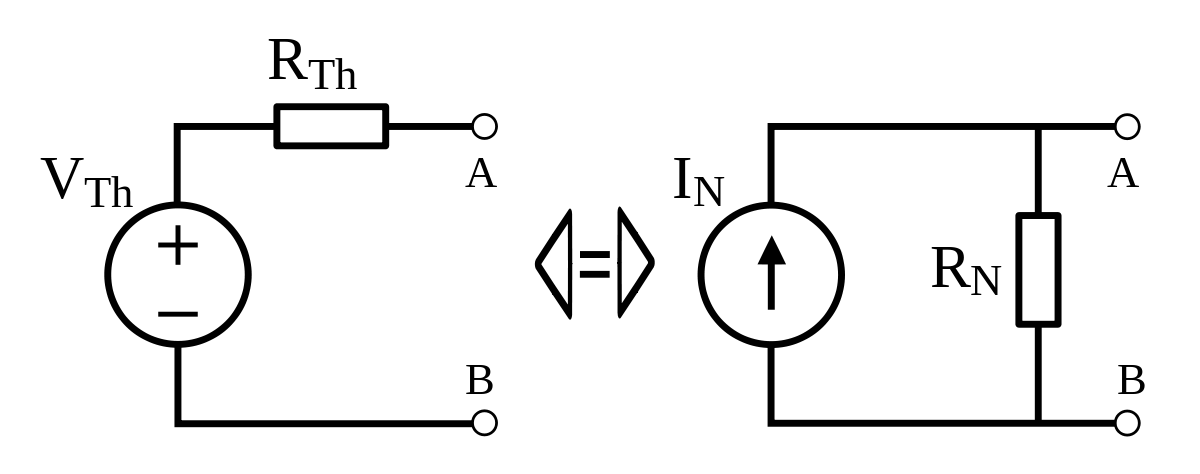
Conversion entre un circuit de Thévenin et de Norton

Circuit de Thévenin (à gauche) et circuit de Norton (à droite).

On passe directement d'un circuit de Thévenin à un circuit de Norton et inversement, à l'aide des formules suivantes:

• De Thévenin à Norton;

• De Norton à Thévenin;