Théorème des fonctions implicites - Définition

Démonstration

Existence de la fonction φ

La démonstration proposée ici ne concerne que le deuxième énoncé. On se place ici dans le contexte des notations utilisées. Le principe consiste à traduire la question sous une forme telle qu'il devient possible d'appliquer le théorème d'inversion locale. On considère l'application ψ₁, de UxV dans ExG, définie par :

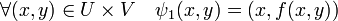
Cette application est de classe C^p et sa différentielle est un isomorphisme bicontinu, il est possible d'appliquer le théorème d'inversion locale qui montre l'existence d'un ouvert WxX de FxG et d'une application φ₁ vérifiant:

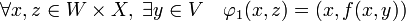
On définit φ comme l'application de W dans F, qui à x de W associe φ₁(x, 0). L'application φ est de classe C^p car φ₁ l'est, d'après le théorème d'inversion locale et par construction, f(x, φ(x)) est bien égal à 0.

Comme on peut le remarquer, ce théorème peut être vu comme une conséquence presque directe de celui de l'inversion locale.

Unicité de la fonction φ

L'objectif est maintenant de montrer que les deux fonctions φ₁ et φ₂ de l'énoncé sont bien confondues sur U₀. Soit x un élément de de U₀ et h désigne le vecteur x - x₀. On recherche l'ensemble C des réels t compris entre 0 et 1 tels que si τ est compris entre 0 et t, φ₁(x₀ + τh) et φ₂(x₀ + τh) soient confondus.

Comme U₀ est convexe, les expressions sont bien définies. Par construction l'ensemble C est un connexe de [0, 1]. Il est non vide car il contient 0. Comme φ₁ et φ₂ sont continues, l'ensemble C contient sa borne supérieure et c'est un fermé. Montrons qu'il est aussi ouvert. Soit s un élément de C, φ₁(x₀ + sh) et φ₂(x₀ + sh) sont égaux. On peut appliquer le théorème sur le point x₀ + sh, la fonction équivalente à ψ₁ (mais cette fois définie sur un voisinage de x₀ + sh) est une bijection, ce qui montre que si z est dans un voisinage de x₀ + sh, le point (z, 0) admet un unique antécédent, qui est nécessairement la valeur de φ₁(z) ainsi que celle de φ₂(z). Ce qui montre qu'il existe un ouvert contenant s inclus dans C.

Le seul ensemble non vide, ouvert et fermé d'un connexe est l'ensemble tout entier, on en déduit que C est égal à [0, 1]. Autrement dit, 1 est élément de C, ou encore φ₁ et φ₂ ont la même valeur en x, ce qui termine la démonstration.