Théorème des fonctions implicites - Définition

Introduction

En mathématiques, le théorème des fonctions implicites est un résultat de géométrie différentielle. Certaines courbes sont définies par une équation cartésienne, c'est-à-dire la forme f(x, y) = 0, où x et y décrivent les nombres réels. Le théorème indique que si la fonction f est suffisamment régulière au voisinage d'un point de la courbe, il existe une fonction φ, telle que localement, la courbe et le graphe de la fonction φ sont confondus. Plus précisément, si (x₀, y₀) vérifie l'équation, si f est continûment différentiable et que sa dérivée partielle en (x₀, y₀) n'est pas nulle, alors il existe un voisinage de (x₀, y₀) sur lequel la zone s'identifie au graphe de φ.

Ce théorème admet une variante plus générale, qui s'applique non plus au plan, mais à des espaces de Banach, c'est-à-dire des espaces vectoriels complets. Ce résultat est une forme équivalente du théorème d'inversion locale qui indique qu'une fonction différentiable et suffisamment régulière est localement inversible, c'est une conséquence directe d'un théorème du point fixe.

Ce théorème se trouve dans différentes branches des mathématiques, sous cette forme ou sous celle de l'inversion locale. Il permet de démontrer le mécanisme des multiplicateurs de Lagrange, il intervient dans un contexte plus géométrique, pour l'étude des variétés différentielles, on le trouve encore pour l'étude des équations différentielles où il est, entre autres, utilisé à travers le théorème du redressement d'un flot, permettant de démontrer le théorème de Poincaré-Bendixson. Il dépasse le cadre des mathématiques, les physiciens ou les économistes en font usage, lorsque certaines variables ne peuvent être définies à l'aide d'une fonction, mais uniquement implicitement à l'aide d'une équation.

Énoncés

Selon les besoins, on trouve des énoncés différents de ce théorème. En dimension deux, il prend la forme suivante :

• Soit f(x, y) une fonction de classe C^p définie sur un ouvert U de R² et à valeurs dans R. Soit (x₀, y₀) un point de U tel que f(x₀, y₀) = 0 et tel que la dérivée partielle de f, par rapport à la deuxième variable, ne soit pas nulle en (x₀, y₀). Il existe un ouvert V contenu dans U et contenant (x₀, y₀) et une fonction φ de classe C^p et de R dans R, tels que l'équivalence suivante soit vraie :

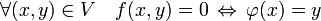
(La condition φ(x₀)=y₀ n'est pas explicitée dans ce premier énoncé, car elle n'est qu'un cas particulier de l'équivalence.) La dérivée de φ au point x₀ est donnée par la formule :

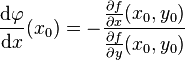
Cette version n'est pas toujours satisfaisante. Il peut être utile d'utiliser ce résultat sur des surfaces et non plus sur des courbes, voire sur des espaces vectoriels dont la dimension n'est pas nécessairement finie. On trouve cette version plus sophistiquée:

• Soient E, F et G trois Banach, U un ouvert de E, V un ouvert de F, f une application de classe C^p de UxV dans G et (x₀, y₀) un point de UxV tel que f(x₀, y₀) = 0 et tel que la différentielle partielle D₂f(x₀, y₀) soit une bijection bicontinue de F dans G.

• Il existe un ouvert U₀ de U contenant x₀ et une application φ, de classe C^p, définie sur U₀ telle que :

.

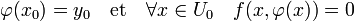
• En outre, sur tout ouvert convexe U₀ de U contenant x₀, il existe au plus une application continue φ vérifiant les deux conditions précédentes.