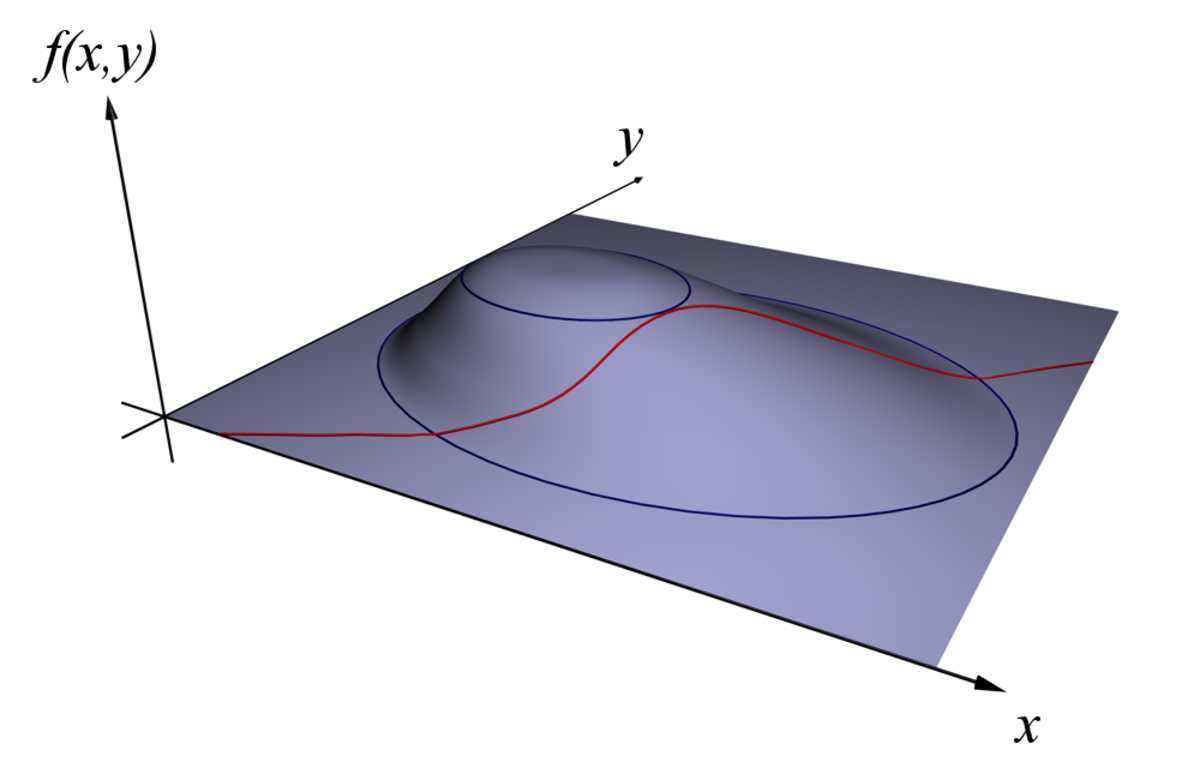
Théorème des fonctions implicites - Définition

Dimension supérieure

Multiplicateur de Lagrange

La méthode des multiplicateurs de Lagrange permet de trouver un optimum, tout en satisfaisant une contrainte. Sur la figure, on cherche le point le plus élevé possible, située sur la ligne rouge.

Le théorème des fonctions implicites peut aussi être vu comme un outil pour démontrer des résultats, à l'image de la méthode du multiplicateur de Lagrange. On se place ici dans Rⁿ, on cherche les optimums d'une fonction f d'un ouvert U de Rⁿ dans R, vérifiant une contrainte g(x) = 0. On suppose ici que f et g sont continument différentiables. Pour plus de simplicité, on suppose que la contrainte définit une surface de dimension n - 1, c'est-à-dire que g est une fonction dont la différentielle est injective en chaque point et que g est à valeurs dans R. Le cas général est traité dans l'article détaillé.

Le théorème associé au multiplicateur de Lagrange indique que les gradients en de f et de g sont colinéaires sur les extrema recherchées. Le théorème des fonctions implicites permet simplement de montrer ce résultat dans le cadre des hypothèses restrictives choisies ici. Soit a un tel extremum, on note grad_g(a) le gradient de g au point a. Si V désigne un voisinage de a inclus dans U, on peut écrire tout vecteur de v sous la forme a + h + λ.grad_g(a), ou h est un vecteur orthogonal au gradient et λ une valeur scalaire. La contrainte g(x) = 0 s'exprime sur V par l'équation φ(h, λ) = g(a + h + λ.grad_g(a)) = 0. Un rapide calcul montre que la différentielle partielle sur λ est égale au carré de la norme du gradient, qui par hypothèse n'est pas nul. Le théorème des fonctions implicites permet de considérer localement la contrainte comme respecté par les points images par une fonction ψ d'un ouvert de R^n-1 dans R. Plus précisément, il existe un voisinage W du vecteur nul de l'hyperplan orthogonal au gradient de g tel que les points de la contraintes s'écrivent de manière unique sous la forme a + h + ψ(h).grad_g(a), avec h élément de W. Dire que a est un extremum signifie que la fonction f₁ qui à h associe f(a + h + ψ(h).grad_g(a)) admet une différentielle nulle en 0. On obtient :

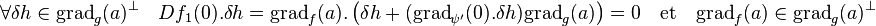
Les seuls vecteurs orthogonaux à l'orthogonal d'un vecteur non nul sont les vecteurs colinéaires, ce qui montre la propriété.

Variété différentielle

Une variété différentielle de dimension d de Rⁿ où n et d sont des entiers strictement positifs tel que d est plus petit que n, permet de généraliser les notions de courbes ou de surfaces lisses et régulières de dimension 2. Les termes de lisse et régulier sont des métaphores pour désigner le fait que les êtres considérés n'ont pas d'arête ou de point double. L'objet de ce paragraphe concerne les figures à l'image d'une sphère, qui est une variété différentielle de dimension 2, mais pas d'un cube, qui contient des points singuliers.

Le voisinage d'un point O d'une variété de dimension d possède la propriété d'être semblable, au sens du difféomorphisme, à un ouvert de R^d. On peut l'exprimer de la manière suivante : il existe un ouvert U de R^d et une bijection bicontinue φ₁, continument différentiable de U dans un ouvert de la variété contenant le point O et la différentielle en un point quelconque est de rang d. Autrement dit, il existe un bon paramétrage du voisinage de O. Il est aussi possible d'exprimer cette propriété à l'aide d'une équation cartésienne. Il existe un ouvert V de Rⁿ et une fonction ψ de V dans R^n-d continument différentiable et dont les différentielles sont surjectives, tel que l'intersection de la variété avec V soit l'ensemble des points x qui vérifie l'équation ψ₁(x) = 0, ce qui donne une définition locale à l'aide d'une équation cartésienne

Cette situation est la copie d'une configuration classique en algèbre linéaire. Un sous-espace vectoriel de dimension d d'un espace de dimension n peut être vu, soit comme l'image d'une application linéaire injective d'un espace de dimension d, soit comme le noyau d'une application surjective dans un espace de dimension n - d. En algèbre linéaire, ces deux points de vue sont équivalents. Il en est de même avec les variétés différentielles. L'équivalence ce démontre dans un sens avec le théorème des fonctions implicites, la réciproque est plus aisée avec le théorème d'inversion locale.

Supposons que l'on dispose d'une équation paramétrique ψ₁(x) = 0 sur le voisinage U. La différentielle de ψ₁ en x₀, coordonnées du point O, est de rang d et possède un noyau K de dimension n - d et un supplémentaire H de ce noyau de dimension d, d'après le théorème du rang. Tout élément de U s'écrit de manière unique comme égal à une somme x₀ + h + k et l'on peut choisir un ouvert U_H de H contenant le vecteur nul et un ouvert U_K de H contenant le vecteur nul tel que x₀ + U_H + U_K soit contenu dans U. L'application ψ de U_HxU_K dans R^d, qui à (h, k) associe ψ₁(x₀ + h + k) satisfait aux hypothèses du théorème des fonctions implicites, d'où l'existence d'un paramétrage locale du voisinage de O, construit sur le voisinage U_H.

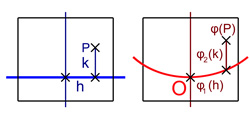
On suppose maintenant que l'on dispose d'une représentation paramétrique locale du voisinage de O, c'est-à-dire une application φ₁ de R^d dans Rⁿ dont l'image est un voisinage de O dans la variété. Cette situation est illustrée sur la figure de droite. La droite bleue représente R^d, la portion de courbe la variété contenant le point O est représentée en rouge. On identifie R^d avec le sous-espace vectoriel de Rⁿ dont les n - d dernières coordonnées sont nulles. L'image de la différentielle de φ₁ au point x₀ est un sous-espace vectoriel de dimension d, on considère H_a un supplémentaire de ce sous-espace vectoriel. On appelle H_d le sous-espace de Rⁿ ayant les d premières coordonnées nulles. Les sous-espaces H_a et H_d ont même dimensions, ils sont donc isomorphes, soit φ₂ un tel isomorphisme. On considère maintenant φ l'application de UxH_d dans Rⁿ, qui à x₀ + h + k associe φ₁(x₀ + h) + φ₂(k). Ici h désigne un vecteur de R^d et k un vecteur de H_a. L'application φ est continument différentiable et sa différentielle au point x₀ est un isomorphisme. Le théorème d'inversion locale montre qu'il existe un ouvert W contenant O et une application ψ₁ de W dans Rⁿ différentiable et qui soit localement une réciproque de φ. L'image de l'intersection de la variété et de W est incluse dans H_d, si l'ouvert W est choisi suffisamment petit. Il suffit de composer ψ₁ par l'application linéaire qui à un vecteur de Rⁿ, associe le vecteur de R^n-d composée des n - d dernières coordonnées du vecteur d'origine, pour conclure. Si ψ est cette application composée, sur un voisinage de O, la variété est définie par l'équation ψ(x) = 0.

Théorème du redressement d'un flot

Le théorème des fonctions implicites joue un rôle pour l'étude des équations différentielles. On le trouve à divers endroits, dont le théorème du redressement d'un flot. Considérons l'équation différentielle autonome (1) :

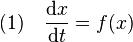
Ici f désigne une fonction continument différentiable définie sur U, un ouvert d'un espace de Banach E et à valeurs dans E. Le théorème de Cauchy-Lipschitz montre l'existence d'une unique fonction flot φ qui prend ses valeurs dans un ouvert V inclus dans RxU et à valeur dans E, telle que la fonction qui à t associe φ(t, x) soit l'unique solution de l'équation (1) avec la condition de Cauchy s(0) = x.

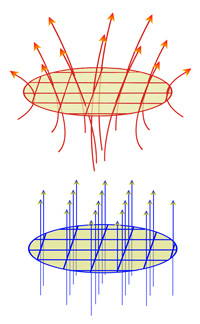
Un exemple de flot, au voisinage V₁ d'un point x₀ de U est illustré en rouge à droite. Si l'on considère l'intersection de V₁ avec un hyperplan affine contenant x₀ et dont la direction ne contient pas f(x₀), on obtient la pastille illustrée en rouge et jaune. Pour l'étude locale d'un flot, la configuration équivalente au dessous, en bleu est plus simple. Si la fonction f est constante, sur un voisinage de la pastille V, pour un point x de V, les solutions de l'équation différentielle (1) sont décrites par le flot φ(t, x) = x + t.v où v est le vecteur constant image de f, sur un voisinage de V.

Une conséquence de l'article est l'existence d'un difféomorphisme ψ définie sur un voisinage Wx]-μ, μ[ de x tel que :

Autrement dit, il est possible de redresser le flot φ à l'aide d'un difféomorphisme ψ, ce qui permet une étude locale plus aisée de l'équation différentielle (1). La démonstration de ce résultat est fondé sur le fait que la fonction flot est aussi continument différentiable. La restriction φ de Wx]-μ, μ[ possède au point (0, x₀) une différentielle inversible et bicontinue. Le théorème d'inversion locale permet de conclure. Ce résultat est utilisé, par exemple dans la démonstration du théorème de Poincaré-Bendixson

Théorème de Cauchy-Lipschitz

Le théorème précédent est une application directe du théorème d'inversion locale, à la condition de disposer d'un résultat non immédiat. Si la fonction f du paragraphe précédent est de classe C¹, alors le flot l'est aussi. Ce résultat porte généralement le nom de théorème de Cauchy-Lipschitz. Cette forme sophistiquée du théorème est traitée dans l'article détaillé. De manière indépendante, deux mathématiciens Pugh et Robbin ont trouvé une même démonstration élémentaire. Elle consiste à étudier l'application T qui à un couple (x, σ) associe une fonction. Ici x est un élément de U avec les notations du paragraphe précédent et σ une fonction d'un petit intervalle contenant O. L'application est définie de la manière suivante :

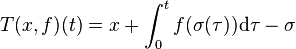
La solution intégrale s, qui à t associe φ(t, x) vérifie l'égalité T(x,s) = 0. Il est relativement simple de montrer que T satisfait les hypothèses du théorème des fonctions implicites, ce qui montre que la fonction qui à x associe la courbe intégrale φ(t, x) est de classe C¹. A partir de là, il est simple d'en déduire le caractère C¹.

Cet démonstration montre la pertinence du deuxième énoncé, très général, du théorème des fonctions implicites proposé dans cet article. En analyse fonctionnelle et à l'image du résultat de ce paragraphe, il n'est pas inutile de bénéficier de la généralité que confère le fait de choisir les variables dans un Banach.