Tonneau (formules) - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Volume partiel en fonction de la hauteur de liquide
La génératrice est la parabole d'équation :
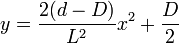
- Pour un tonneau couché
Soit h la hauteur de liquide
Soit x1 et x2 les bornes maximales selon les valeurs de h
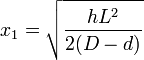
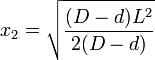
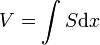
Où S représente le segment circulaire, de rayon y, de flèche
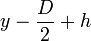
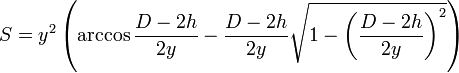
Si
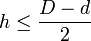
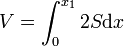
Si
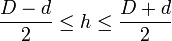
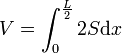
Si
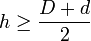
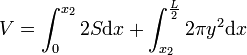
- Pour un tonneau debout
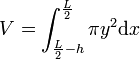
![\begin{align}V&=\pi\Biggl[\frac{4(d-D)^2}{5L^4}\left(\left(\frac L2\right)^5-\left(\frac L2-h\right)^5\right) \\ \ & +\frac{2D(d-D)}{3L^2}\left(\left (\frac L2\right)^3-\left(\frac L2-h\right)^3\right)+h\left(\frac D2\right)^2 \Biggr ] \end{align}](https://static.techno-science.net/illustration/Definitions/autres/1/1c04c37493a4cf55f5c597a27143ab3f_ea9d2321918aa3e7688f0157479ffdd9.png)

















































