Tonneau (formules) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Quelques formules historiques - Tonneau à section elliptique - Calcul - Surfaces - Volume partiel en fonction de la hauteur de liquide

Introduction

Pour trouver la capacité d'un tonneau, ou jaugeage, beaucoup de formules ont été proposées, mais aucune ne donne exactement le volume. Après un rappel historique des différents auteurs, d'autres formules seront expliquées et proposées. Des formules complémentaires, en fonction de la hauteur de liquide, ou encore relatives aux surfaces, seront également présentées.

Quelques formules historiques

Tonneau couché

Kepler a donné une formule approchée

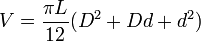
$V = \frac {\pi L} {12} (D^2+Dd+d^2)$

Oughtred a modifié la formule :

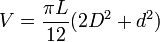
$V = \frac {\pi L}{12} (2D^2+d^2)$

Une instruction du ministère de l’intérieur en pluviôse de l’an VII fixa la formule suivante :

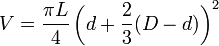
$V = \frac {\pi L}{4} \left( d + \frac 23 (D-d) \right)^2$

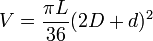
Ou encore : $V = \frac {\pi L}{36} (2D+d)^2$

Dez a établi la formule :

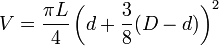
$V = \frac {\pi L}{4}\left( d + \frac 38 (D-d) \right)^2$

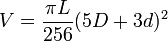
Ou encore : $V = \frac {\pi L}{256} (5D+3d)^2$

Les Douanes emploient la formule :

$V = 0,625 C 3$

Dans laquelle $C$ représente la diagonale allant du trou de bonde au point le plus éloigné de ce trou. Elle est très rapide, car elle n’exige qu’une seule mesure. On peut même avoir immédiatement le volume en marquant sur une règle les volumes calculés d’après les $C$ correspondants.

Tonneau à section elliptique

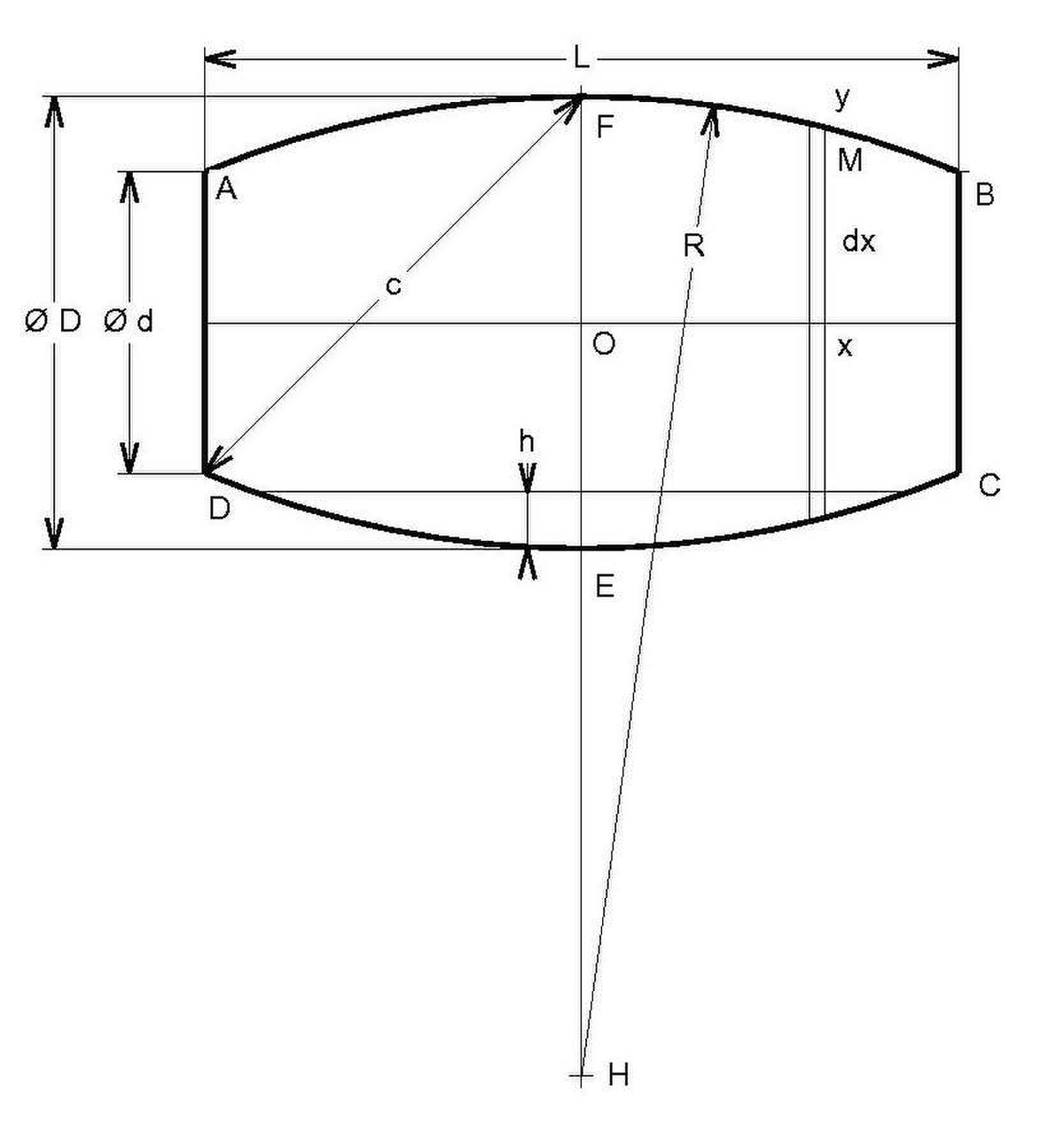
Soient A et B les diamètres de la section elliptique du bouge, et soient a et b les diamètres des fonds.

Si on a des paraboles comme génératrices, on a les formules :

Dans le plan x0y :

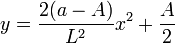
$y=\frac{2(a-A)}{L^2}x^2+\frac A2$

Dans le plan x0z :

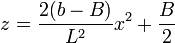
$z=\frac{2(b-B)}{L^2}x^2+\frac B2$

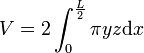
$V=2\int_0^\frac L2 \pi yz\mathrm dx$

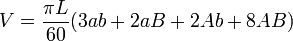
$V=\frac{\pi L}{60}(3ab+2aB+2Ab+8AB)$

Si on a des ellipses comme génératrices

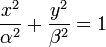
Dans le plan xOy on a l’ellipse $\frac{x^2}{\alpha^2}+\frac{y^2}{\beta^2}=1$

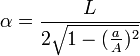
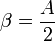
Où $\alpha=\frac{L}{2\sqrt{1-(\frac aA)^2}}$ et $\beta=\frac A2$

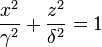
Dans le plan xOz on a l’ellipse $\frac{x^2}{\gamma^2}+\frac{z^2}{\delta^2}=1$

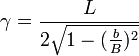
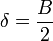
Où $\gamma=\frac{L}{2\sqrt{1-(\frac bB)^2}}$ et $\delta=\frac B2$

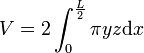
$V=2\int_0^\frac L2 \pi yz\mathrm dx$

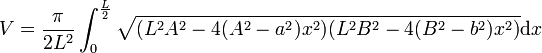
$V=\frac{\pi}{2L^2} \int_0^\frac{L}{2}\sqrt{(L^2A^2-4(A^2-a^2)x^2)(L^2B^2-4(B^2-b^2)x^2)}\mathrm dx$

Calcul

La forme générale des tonneaux consiste en une surface de révolution engendrée par une portion de courbe et terminée par deux plans parallèles équidistants de l’équateur. Cette courbe génératrice passe par trois points.

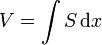
$V = \int S\, \mathrm dx$

Où $S$ est la surface du disque de rayon $y$

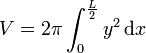
$V = 2\pi\int_0^{\frac{L}{2}} y^2\, \mathrm dx$

Exemples :

Parabole

C'est une courbe passant par trois points très commode en mathématiques.

Et la parabole s’exprime par : $y = a x 2 + b$

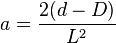
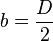
Avec $a=\frac{2(d-D)}{L^2}$ et $b=\frac D2$

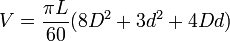
Le polynôme s’intègre facilement, et on obtient : $V=\frac {\pi L} {60} (8D^2+3d^2+4Dd)$

Ellipse

Elle a pour équation :

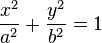
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

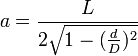
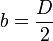
Où $a=\frac{L}{2\sqrt{1-(\frac {d}{D})^2}}$ et $b=\frac {D}2$

D'où la formule

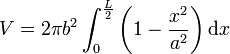
$V=2\pi b^2\int_0^\frac{L}{2}\left(1-\frac{x^2}{a^2}\right)\mathrm dx$ s'intègre facilement elle aussi, et on obtient

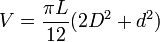
$V=\frac{\pi L}{12}(2D^2+d^2)$

On retrouve la formule d'Oughtred.

Cercle

C'est la courbe qui vient immédiatement à l'esprit, car elle est facile à tracer au compas, mais elle est difficile à manipuler. L'équation s'exprime par :

$x 2 + (y - b) 2 = R 2$

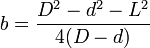
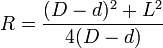
avec $b=\frac{D^2-d^2-L^2}{4(D-d)}$ et $R=\frac{(D-d)^2+L^2}{4(D-d)}$

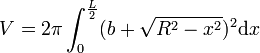
$V=2\pi \int_0^\frac{L}{2}(b+\sqrt{R^2-x^2})^2\mathrm dx$

Droite

Plus simplement on peut prendre deux droites génératrices. On obtient deux troncs de cône.

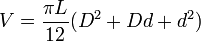
$V = \frac {\pi L} {12} (D^2+Dd+d^2)$

C'est la formule de Kepler.

Résistance des matériaux

Une poutre sur deux appuis simples ou une poutre encastrée se déforme en flexion selon une courbe :

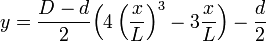
$y=\frac {D-d}{2}\Bigl(4\left(\frac{x}{L}\right)^3-3\frac{x}{L}\Bigr)-\frac{d}{2}$

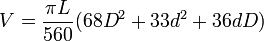
$V=\frac{\pi L}{560}(68D^2+33d^2+36dD)$

Autres formules

Cosinus

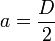
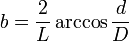
$y = a cos b x$ avec $a=\frac{D}{2}$ et $b=\frac{2}{L}\arccos \frac{d}{D}$

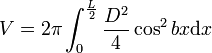
$V=2\pi\int_0^\frac{L}{2} \frac{D^2}{4} \cos^2 bx\mathrm dx$

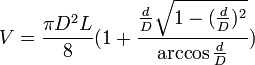
$V=\frac{\pi D^2 L}{8}(1+\frac{\frac {d}{D}\sqrt{1-(\frac{d}{D})^2}}{\arccos \frac{d}{D}})$

Cosinus hyperbolique

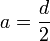
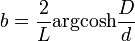
$y = a cosh b x$ avec $a=\frac{d}{2}$ et $b=\frac{2}{L} \operatorname{argcosh} \frac{D}{d}$

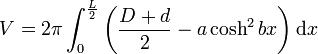
$V=2\pi\int_0^\frac{L}{2} \left(\frac{D+d}{2}-a\cosh^2 bx\right)\mathrm dx$

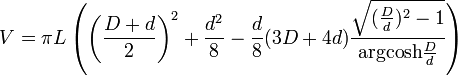
$V=\pi L\left (\left(\frac{D+d}{2}\right)^2+\frac{d^2}{8}-\frac{d}{8}(3D+4d)\frac{\sqrt{(\frac{D}{d})^2-1}}{\operatorname{argcosh}\frac{D}{d}}\right)$

Hyperbole

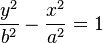
$\frac{y^2}{b^2}-\frac{x^2}{a^2}=1$

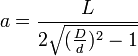
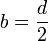
Où $a=\frac{L}{2\sqrt{(\frac{D}{d})^2-1}}$ et $b=\frac{d}{2}$

$\begin{align}V&=\pi L\Bigg[\left(\frac{D+d}{2}\right)^2+\frac{d^2}{6}+\frac{D^2}{12} \\ \ & -\frac{d(D+d)}{4\sqrt{\left(\frac{D}{d}\right)^2-1}}\left(\frac{D}{d}\sqrt{\left(\frac{D}{d}\right)^2-1}+\operatorname{argsinh} \sqrt{\left(\frac{D}{d}\right)^2-1}\right)\Bigg]\end{align}$

Surfaces

On considère ici aussi la parabole comme génératrice. Soit $S 1$ cette surface

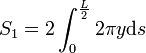
$S_1=2\int_0^\frac{L}{2} 2\pi y\mathrm ds$

où $d s$ est la différentielle de l'abscisse curviligne.

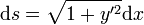
$\mathrm ds=\sqrt{1+y'^2}\mathrm dx$

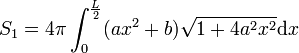
$S_1=4\pi\int_0^\frac L2(ax^2+b)\sqrt{1+4a^2x^2}\mathrm dx$

L'intégration se fait par le changement de variable : $2 a x = sinh t$

On arrive à :

$\begin{align} S_1& =\frac{\pi L} {4}\Biggl[\sqrt{\frac{4(d-D)^2}{L^2}+1}\left ( d+D +\frac{L^2}{8(d-D)}\right) \\ \ & +\frac{L}{d-D}\left(D-\frac{L^2}{16(d-D)}\right)\operatorname{argsinh}\frac{2(d-D)}{L}\Biggr]\end{align}$

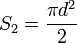
Puis on ajoute les deux fonds : $S_2=\frac{\pi d^2}{2}$

$S = S 1 + S 2$

Surfaces partielles

Surface du tonneau en contact avec le liquide

Tonneau couché

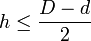
Si $h\le\frac{D-d}{2}$ , alors

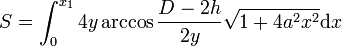
$S=\int_0^{x_1} 4y \arccos\frac{D-2h}{2y}\sqrt{1+4a^2x^2}\mathrm dx$

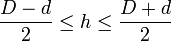
Si $\frac{D-d}{2}\le h \le \frac{D+d}{2}$ , alors

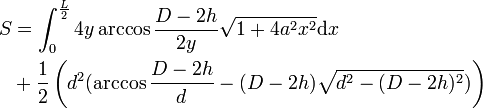
$\begin{align} S&=\int_0^\frac{L}{2} 4y \arccos\frac{D-2h}{2y}\sqrt{1+4a^2x^2} \mathrm dx \\ \ & +\frac 12\left(d^2(\arccos \frac{D-2h}{d}-(D-2h)\sqrt{d^2-(D-2h)^2})\right) \end{align}$

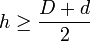
Si $h\ge\frac{D+d}{2}$ , alors

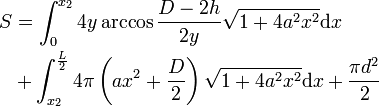
$\begin{align}S&=\int_0^{x_2} 4y \arccos\frac{D-2h}{2y}\sqrt{1+4a^2x^2}\mathrm dx \\ \ & + \int_{x_2}^\frac{L}{2} 4\pi \left(ax^2+\frac D2\right)\sqrt{1+4a^2x^2}\mathrm dx +\frac{\pi d^2}{2}\end{align}$

Tonneau debout

$0 < h < L$ et en tenant compte d'un fond :

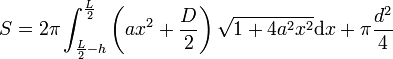
$S=2\pi\int_{\frac L2-h}^\frac L2\left(ax^2+\frac D2\right)\sqrt{1+4a^2x^2}\mathrm dx +\pi \frac{d^2}{4}$

Si $h = 0$ alors $S = 0$ . Et si $h = L$ le tonneau est plein. Voir supra.

$\begin{align} S&=\frac{\pi L}{8} \Biggl[ \sqrt{\frac{4(d-D)^2} {L^2} + 1 } \left( d+D + \frac{L^2}{8(d-D)}\right) \\ \ & - \frac{L-2h}{L}\sqrt{\frac {4(d-D)^2(L-2h)^2}{L^4}+1} \left(\frac{(d-D)(L-2h)^2}{L^2}+\frac{L^2}{8(d-D)} +2D\right) \\ \ & + \frac{L}{d-D}\left(D-\frac{L^2}{16(d-D)}\right)\left(\operatorname{argsinh}\frac{2(d-D)}{L^2}-\operatorname{argsinh}\frac{2(d-D)(L-2h)}{L^2}\right)\Bigg] \\ \ & +\frac{\pi d^2}{4}\end{align}$

Surface de liquide en contact avec l'air

Tonneau couché

La génératrice est la parabole.

La corde $c$ au point d'abscisse $x$ s'exprime par :

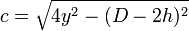
$c=\sqrt{4y^2-(D-2h)^2}$

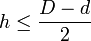
Si $h\le\frac{D-d}{2}$ ,

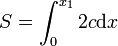
$S=\int_0^{x_1} 2c \mathrm dx$

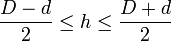
Si $\frac{D-d}{2}\le h \le \frac{D+d}{2}$ , alors

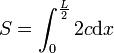
$S=\int_0^\frac L2 2c \mathrm dx$

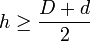
Si $h\ge\frac{D+d}{2}$ , alors

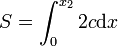
$S=\int_0^{x_2} 2c\mathrm dx$

Tonneau debout

La génératrice est la parabole

$0 < h < L$

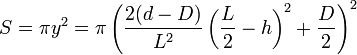
$S=\pi y^2=\pi\left( \frac{2(d-D)}{L^2}\left(\frac L2-h\right)^2+\frac D2\right)^2$

Si $h = 0$ le tonneau est vide, et si $h = L$ le tonneau est plein.

Volume partiel en fonction de la hauteur de liquide

- Introduction - Quelques formules historiques - Tonneau à section elliptique - Calcul - Surfaces - Volume partiel en fonction de la hauteur de liquide

Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟

Cette astuce simple réduit la consommation d'alcool... des femmes 🍷

Découverte: la lumière transforme un isolant en métal 💡

Cet aliment à bannir nourrit les cancers 🍽️

Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️

Découverte d'une chimie des océans refroidissant le climat 🌊

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Ce plat millénaire réduit significativement la graisse corporelle 🍽️

Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭

Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠

De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽

Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️

Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐

Une montagne d'or découverte en Chine ⛏️

Cette simulation de l'Univers est totalement vertigineuse 🌀

Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘

Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️

Page générée en 0.456 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise