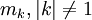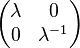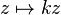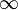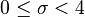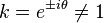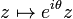Transformation de Möbius - Définition
La liste des auteurs de cet article est disponible ici.
Les transformations de Möbius du plan complexe
Forme générale
Les transformations de Möbius conservant l'orientation sont de la forme
-
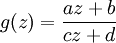
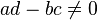
Réciproquement une telle fonction est bien une transformation de Möbius par composition des fonctions suivantes (
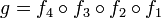
-
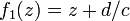
-
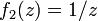
-
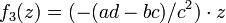
-
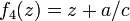
Détermination d'une transformation de Möbius du plan
La résolution de g(z)=z montre qu'une transformation de Möbius est uniquement déterminée par l'image qu'elle donne de trois points distincts. Mieux, si z1,z2 et z3 sont des points tous distincts ainsi que w1,w2,w3, alors il existe une unique transformation de Möbius
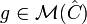
Pour montrer l'existence de g, il suffit de "déplacer" les points en composant g avec d'autres transformations. La transformation de Möbius
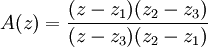
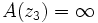
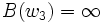
Représentation par des matrices
On remarque que à la matrice
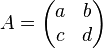
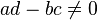
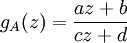
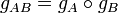
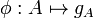
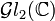
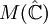
De plus, pour tout
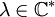
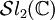
Extension de Poincaré
Nous avons vu dans les propriétés générales que les transformations de Möbius admettent une extension de Poincaré. Nous allons l'expliciter dans le cas d'une transformation du plan complexe en considérant
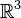

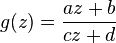
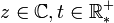
Classification
En résolvant l'équation g(z) = z, on s'aperçoit qu'une transformation de Möbius du plan ne peut admettre que 1 ou 2 points fixes, ce qui pourrait être un critère de classification. Cependant, un critère plus précis est le nombre de points fixes de leur extension de Poincaré (1, 2 ou une infinité): si on définit les transformations normales mk,
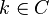
-
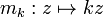
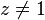
-
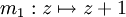
on s'aperçoit que chaque transformation de Möbius est conjuguée à une unique transformation normale mk, avec k = 1 ssi
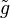
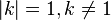
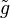
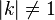
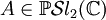
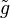
| Transformation | Points fixes de
| Trace au carré σ | Forme normale | Représentant | |
|---|---|---|---|---|---|
| Parabolique | 1 | σ = 4 | m1 |
|
|
| Loxodromique | 2 |
|
k = λ2,λ − 2 |
|
|
| Elliptique |
|
| mk, | k | = 1, |
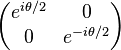
|
|
On peut encore affiner cette classification dans le cas loxodromique: g sera hyperbolique si sa trace au carré est réelle, strictement loxodromique dans le cas contraire.
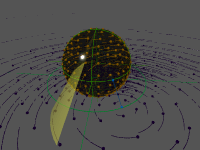
Projection stéréographique
La projection stéréographique envoie le plan complexe sur la sphère de Riemann, sur laquelle on aperçoit plus aisément l'action des transformations de Möbius, comme en témoignent les représentations suivantes.
| Elliptique | Hyperbolique | Loxodromique | |
| Un point fixe à l'infini |
|

|

|
| Points fixes diamétralement opposés |
|

|

|
| Points fixes arbitraires |

|

|

|
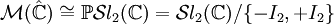
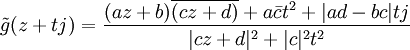
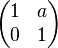
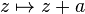
![\sigma\in\mathbb C, \sigma \not\in [0,4]](https://static.techno-science.net/illustration/Definitions/autres/6/62b7bac029f220a0f97382254ded4939_d23a16291f8db7075e58a4fbb0e830fd.png)