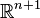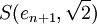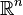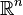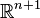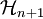Transformation de Möbius - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
- La transformation de Möbius ne doit pas être confondue avec la transformée de Möbius
Les transformations de Möbius sont de manière générale des automorphismes du compactifié d'Alexandrov de
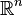
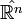
En particulier, si on identifie
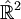
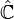
-
-
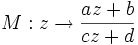
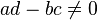
-
On étend alors cette fonction à
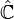
-
-
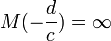
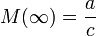
-
Définition générale
Soit
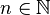
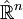
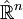
- pour un hyperplan (
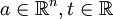
-
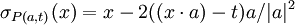
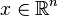
-
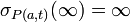
- pour une sphère
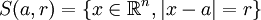
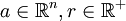
-
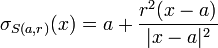
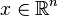
-
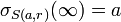
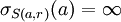
On remarque que les inversions sont involutives: si σ est une inversion, σ2 = Id
De plus, ces inversions sont des homéomorphismes.
- Définition: L'ensemble des transformations de Möbius, est le sous-groupe des homéorphismes de
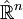
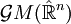
- Définition: Le groupe de Möbius
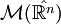
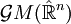
Propriétés générales
Dorénavant, on appelle sphère soit une sphère soit un plan (Beardon, The Geometry Of Discrete Groups). En remarquant que les inversions transforment les sphères en sphères, on obtient:
- Propriété: Les transformations de Möbius transforment les sphères en sphères
ce qui constitue une de leurs caractéristiques fondamentales.
Le théorème suivant est tout aussi important:
- Théorème: Soit Σ une sphère et φ une transformation de Möbius qui fixe chaque point de Σ. Alors soit φ est l'identité, soit φ est l'inversion par rapport à Σ.
Il permet notamment de montrer l'unicité de l' extension de Poincaré d'une transformation
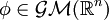
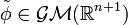
 tel que
tel que
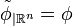
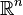
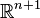
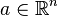
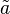
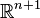
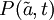
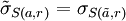
- Propriété: L'extension de Poincaré de
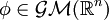
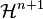
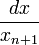
Exemples de transformations de Möbius
Les principaux exemples de transformations de Möbius sont:
- Les translations (par composition de deux réflexions)
- Les isométries de
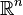
- Les homothéties 'par composition de deux inversions par rapport à des sphères puis d'une isométrie)
Une transformation de Möbius particulière est très utile en géométrie hyperbolique: l'inversion dans