Transformée de Fourier rapide - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Formulation mathématique - Autres algorithmes - L'algorithme de Cooley-Tukey - Problèmes numériques et approximations - Algorithmes spécialisés dans le traitement de données réelles ou/et symétriques

L'algorithme de Cooley-Tukey

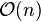
Il s'agit d'un algorithme fréquemment utilisé pour calculer la transformation de Fourier rapide. Il se base sur une approche de type « diviser pour régner » par le biais d'une récursion. Celle-ci subdivise une transformation de Fourier discrète d'une taille composite n = n₁n₂ en plusieurs transformées de Fourier discrètes de tailles inférieures n₁ et n₂. Cet algorithme nécessite $\mathcal{O}(n)$ multiplications par des racines d'unité, plus communément appelés facteurs de rotation.

C'est en 1965 que James Cooley et John Tukey publient cette méthode mais il a été découvert par la suite que l'algorithme avait déjà été inventé par Carl Friedrich Gauss en 1805 et adapté à plusieurs reprises sous des formes différentes.

L'utilisation la plus classique de l'algorithme de Cooley-Tukey est une division de la transformation en deux parties de taille identique $n / 2$ et ceci à chaque étape. Cette contrainte limite les tailles possibles, puisque celles-ci doivent être des puissances de deux. Toutefois, une factorisation reste possible (principe déjà connu de Gauss). En général, les implémentations essaient d'éviter une récursion pour des questions de performance. Il est aussi possible de mélanger plusieurs types d'algorithme lors des subdivisions.

Problèmes numériques et approximations

Tous les algorithmes proposés ci-dessus calculent la transformée sans aucune erreur, de par leur nature analytique. Toutefois, il existe des algorithmes qui peuvent s'accommoder d'une marge d'erreur pour accélérer les calculs. En 1999, Edelman et al. proposent une approximation à la transformée de Fourier rapide. Cette version est destinée à une implémentation en parallèle. Une approximation basée sur les ondelettes est proposée en 1996 par H. Guo et Burrus et tient compte de la répartition dans les entrées/sorties. Un autre algorithme a encore été proposé par Shentov et al. en 1995. Seul l'algorithme de Edelman fonctionne bien avec n'importe quel type de données, il profite de la redondance dans la matrice de Fourier plutôt que de la redondance dans les données initiales.

Toutefois, même les algorithmes décrits de manière analytique présentent des erreurs lorsqu'ils sont implémentés avec des virgules flottantes dont la précision est limitée. L'erreur est cependant limitée. Une borne supérieure d'erreur relative pour Cooley-Tukey est donnée par $O (εlog(n))$ alors qu'elle est de $O (ε n 3 / 2)$ pour la formulation triviale de la transformée de Fourier discrète (Gentleman et Sande, 1966). Le terme $ε$ représente ici la précision relative en virgule flottante. 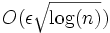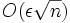En fait, l'erreur quadratique moyenne est encore plus limitée avec seulement $O(\epsilon \sqrt{\log(n)})$ pour Cooley-Tukey et $O(\epsilon \sqrt{n})$ pour la version triviale. Il ne faut malgré tout pas oublier que la stabilité peut être perturbée par les différents facteurs de rotation qui interviennent dans les calculs. Un manque de précision sur les fonctions trigonométriques peut fortement augmenter l'erreur. L'algorithme de Rader est par exemple nettement moins stable que celui de Cooley-Tukey en cas d'erreurs prononcées.

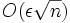
Avec une arithmétique en virgule fixe, les erreurs s'accumulent encore plus vite. Avec Cooley-Tukey, l'augmentation de l'erreur quadratique moyenne est de l'ordre de $O(\epsilon \sqrt{n})$ . De plus, il faut tenir compte de la magnitude des variables lors des différentes étapes de l'algorithme.

Il est possible de vérifier la validité de l'algorithme grâce à une procédure qui vise à déterminer la linéarité et d'autres caractéristiques de la transformation sur des entrées aléatoires (Ergün, 1995).

Algorithmes spécialisés dans le traitement de données réelles ou/et symétriques

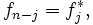
Dans beaucoup d'applications, les données en entrée de la transformation discrète de Fourier sont uniquement des nombres réels. Dans ce cas, les sorties satisfont la symétrie suivante : $f_{n-j} = f_j^*,$

Des algorithmes efficaces ont été conçus pour cette situation, par exemple celui de Sorensen en 1987. Une approche possible consiste à prendre un algorithme classique comme celui de Cooley-Tukey et à enlever les parties inutiles dans le calcul. Cela se traduit par un gain de 50% en mémoire et en vitesse de calcul. 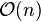Alternativement, il est possible d'exprimer une transformation discrète sur des nombres réels (avec une taille paire) en une transformation avec des nombres complexes mais dont la taille a été divisée par deux (les parties imaginaires sont les éléments impairs et les parties réelles sont les éléments pairs) suivie d'un décodage dont la complexité est de l'ordre de $\mathcal{O}(n)$ opérations.

On pensait que les transformations avec des nombres réels pouvaient être plus efficacement calculées via une transformation discrète de Hartley mais il a été prouvé par la suite qu'une transformation de Fourier discrète modifiée pouvait être plus efficace que la même transformation de Hartley. L'algorithme de Bruun était un candidat pour ces transformations mais il n'a pas eu la popularité escomptée.

Il existe encore d'autres variantes pour les cas où les données sont symétriques (c’est-à-dire des fonctions paires ou impaires) avec un gain supplémentaire de 50%. Dans ce cas, on utilise une transformée en cosinus discret.