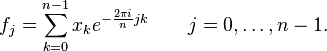Transformée de Fourier rapide - Définition

Introduction

La transformée de Fourier rapide (sigle anglais : FFT ou Fast Fourier Transform) est un algorithme de calcul de la transformée de Fourier discrète (TFD).

Sa complexité varie en avec le nombre de points n, alors que la complexité du calcul de base s'exprime en . Ainsi, pour n=1024, le temps de calcul de l'algorithme rapide peut être 100 fois plus petit que le calcul utilisant la formule de définition de la TFD.

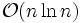
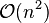
Cet algorithme est couramment utilisé en traitement numérique du signal pour transformer des données discrètes du domaine temporel dans le domaine fréquentiel, en particulier dans les analyseurs de spectre. Son efficacité permet de réaliser des filtrages en passant dans le domaine transformé.

Formulation mathématique

Soient x₀, ...., x_n-1 des nombres complexes. La transformée de Fourier discrète est définie par la formule suivante :

ou en notation matricielle :

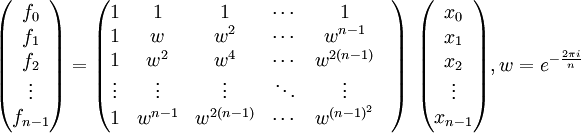
Évaluer ces sommes directement coûte (n − 1)² produits complexes et n(n − 1) sommes complexes alors que seuls (n / 2)(log₂(n) − 2) produits et nlog₂(n) sommes sont nécessaires avec la version rapide. En général, de tels algorithmes dépendent de la factorisation de n mais contrairement à une idée répandue, il y a des transformées de Fourier rapides de complexité pour tous les n, même les n qui sont des nombres premiers.

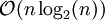
Comme la transformée de Fourier inverse discrète est équivalente à la transformée de Fourier discrète, à un signe et facteur 1/n près, il est possible de générer la transformation inverse de la même manière pour la version rapide.
Remarque : on peut reconnaître ici une matrice de Vandermonde en la matrice n*n.

Autres algorithmes

Il existe d'autres algorithmes qui permettent de calculer la transformée de Fourier rapide. Pour une taille n = n₁n₂, avec des nombres premiers entre eux n₁ et n₂, il est possible d'utiliser l'algorithme PFA (Good-Thomas) basé sur le théorème des restes chinois. Le PFA est similaire à celui de Cooley-Tukey.

L'algorithme de Rader-Brenner est aussi une variante de Cooley-Tukey avec des facteurs de rotation purement imaginaires qui améliorent les performances en réduisant le nombre de multiplications mais au détriment de la stabilité numérique et une augmentation du nombre d'additions. Les algorithmes qui procèdent aussi par des factorisations successives sont ceux de Bruun et l'algorithme QFT. Les versions originales travaillent sur des fenêtres dont la taille est une puissance de deux mais il est possible de les adapter pour une taille quelconque. L'algorithme de Bruun considère la transformée de Fourier rapide comme une factorisation récursive du polynôme zⁿ − 1 en des polynômes avec des coefficients réels de la forme z^m − 1 et z^2m + az^m + 1.

L'algorithme de Winograd factorise zⁿ − 1 en un polynôme cyclotomique, dont les coefficients sont souvent -1,0 ou 1 ce qui réduit le nombre de multiplications. On peut voir cet algorithme comme la version optimale en termes de multiplications. Winograd a montré que la transformée de Fourier discrète peut être calculée avec seulement multiplications, ce qui représente une borne inférieure atteignable pour les tailles qui sont des puissances de deux. Toutefois, des additions supplémentaires sont nécessaires ce qui peut être pénalisant sur les processeurs modernes comportant des unités arithmétiques performantes.

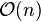
L'algorithme de Rader est quant à lui destiné aux fenêtres dont la taille est un nombre premier. Il profite de l'existence d'une génératrice pour le groupe multiplicatif modulo n. La transformation discrète dont la taille est un nombre premier s'exprime ainsi comme une convolution cyclique d'une taille n − 1. On peut ensuite la calculer par une paire de transformation de Fourier rapide.

Finalement, un autre algorithme destiné aux transformations avec des tailles qui sont des nombres premiers est due à Bluestein. On l'appelle plus souvent l'algorithme chirp-z. Ici encore, la transformation est vue comme une convolution dont la taille est identique à la fenêtre originale. On utilise à cet effet l'identité jk = − (j − k)² / 2 + j² / 2 + k² / 2.