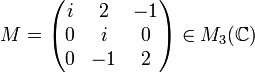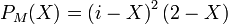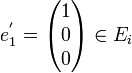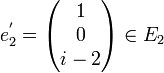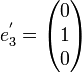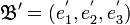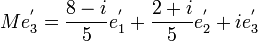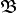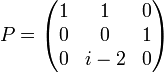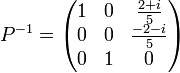Trigonalisation - Définition

Introduction

En algèbre linéaire, trigonaliser une matrice consiste à réduire celle-ci sous la forme d'une matrice triangulaire supérieure, ou inférieure. Ceci n'est possible que sous certaines conditions.

Dans la suite, on se donne un entier naturel et un corps commutatif. désignera l'ensemble des matrices à n lignes et n colonnes à coefficients dans .

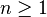
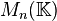
Matrices triangulaires

Une matrice triangulaire supérieure est une matrice dont tous les coefficients situés strictement en dessous de la diagonale sont nuls. En général, on note l'ensemble des matrices triangulaires supérieures. C'est un espace vectoriel, et même mieux, c'est une sous-algèbre de . Une matrice triangulaire supérieure T est donc de la forme :

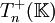
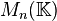
Remarque : De la même manière, une matrice triangulaire inférieure est une matrice dont tous les coefficients situés strictement au-dessus de la diagonale sont nuls.

Conditions de trigonalisation

Il existe plusieurs critères pour savoir si une matrice ou un endomorphisme sont trigonalisables :

• Toute matrice diagonalisable est a fortiori trigonalisable (car une matrice diagonale est un cas particulier de matrice triangulaire).

• Une matrice est trigonalisable si et seulement si son polynôme caractéristique est scindé dans .

En particulier, si est algébriquement clos, toute matrice de est trigonalisable. Cet énoncé est aussi valable pour un endomorphisme de E, espace vectoriel de dimension n sur .

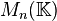
Cas particulier où  : toute matrice de est trigonalisable, car est algébriquement clos (voir théorème de d'Alembert-Gauss).

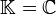
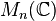
• Un endomorphisme est trigonalisable s'il existe un drapeau de E stable par cet endomorphisme.

Endomorphismes et matrices trigonalisables

Soit , une matrice à n lignes et n colonnes à coefficients dans . On dit que la matrice M est trigonalisable s'il existe une matrice inversible et une matrice triangulaire supérieure telles que :

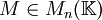
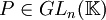
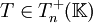
M = PTP ^{− 1} ou bien T = P ^{− 1}MP

Cela revient à dire que M est semblable dans à une matrice triangulaire supérieure.

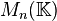
En particulier, toute matrice triangulaire supérieure est trigonalisable, bien évidemment. (Il suffit de choisir P = I_n où I_n est la matrice identité de dimension n.)

Soit E un espace vectoriel sur le corps , de dimension n et u un endomorphisme de E. On dit que u est trigonalisable s'il existe une base de E telle que , où désigne la matrice de l'endomorphisme u dans la base . Autrement dit, un endomorphisme est trigonalisable s'il existe une base dans laquelle sa matrice associée est triangulaire supérieure.

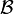
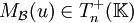
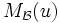
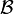
De plus, un endomorphisme est trigonalisable si et seulement si sa matrice dans au moins une base de E est trigonalisable ; dans ce cas, sa matrice dans n'importe quelle base de E est trigonalisable.

Il faut noter un théorème important dû à Schur :

Exemples de trigonalisation

Matrices carrées d'ordre 2 à coefficients réels

Soit une matrice, son polynôme caractéristique est qui a comme unique racine qui est donc l'unique valeur propre de M. L'espace propre associé à la valeur propre est , est donc un sous espace vectoriel de dimension 1 qui a pour base le vecteur . On peut alors compléter avec par exemple le vecteur de manière à ce que forme une base de l'espace tout entier. On sait déjà que et on a facilement , la matrice M dans la base s'écrit donc . On remarquera que la dimension de l'espace propre ne permettait pas ici de diagonaliser la matrice M. La matrice P telle que M = PTP ^{− 1} n'est autre que la matrice de passage de la base canonique à la base , P est donc constituée des vecteurs de exprimés dans la base donc . De même, pour avoir la matrice P ^{− 1} il suffit d'exprimer les vecteurs de dans la base , on a facilement et et donc .

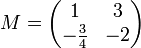
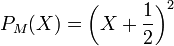
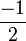
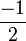
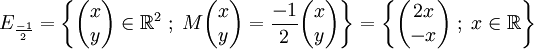
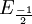
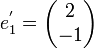
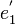
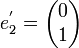
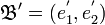
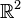
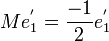
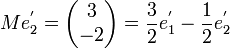
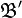
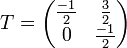
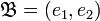
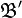
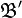
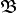
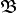
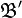
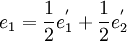
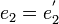
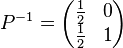
Exemple de trigonalisation d'une matrice carrée d'ordre 3

Soit son polynôme caractéristique est . Comme dans l'exemple précédent on a après calculs : et que l'on complète avec pour former une base de . On remarque que . La matrice M dans la base est donc et l'on a M = PTP ^{− 1} avec P la matrice de passage de la base canonique à la base , P est donc constituée des vecteurs de exprimés dans la base d'où et .