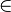Type abstrait - Définition

Introduction

En génie logiciel, un type abstrait est une spécification mathématique d'un ensemble de données et de l'ensemble des opérations qu'elles peuvent effectuer. On qualifie d'abstrait ce type de données car il correspond à un cahier des charges qu'une structure de données doit ensuite implémenter. Notons que la plupart des types abstraits décrivent généralement des structures récursives.

Les types abstraits les plus utilisés sont : pile, file, liste et arbre binaire.

Structure

Un type abstrait est composé de cinq champs :

• TA (Type Abstrait)
• Utilise
• Opérations
• Pré-conditions
• Axiomes

Ces cinq éléments sont souvent réunis sous l'acronyme : TUOPA.

Type Abstrait

Le champ « TA » (Type Abstrait) contient le nom du type que l'on est en train de décrire et précise éventuellement si celui-ci n'est pas une extension d'un autre type abstrait. Par exemple, on écrira « TA : Pile » pour créer un type nommé Pile qui décrit ce qu'est une pile et « Extension TA : Pile » si on désire l'étendre (on étend un type abstrait en lui assignant de nouvelles opérations non définies lors de la première spécification).

Utilise

Le champ « Utilise » contient les types abstraits que l'on va utiliser dans celui que l'on est en train de décrire. Par exemple, le type abstrait Pile que l'on définit va utiliser dans sa spécification le type abstrait Booléen, et on écrira « Utilise : Booléen ».

Opérations

Le champ « Opérations » contient le prototypage de toutes les opérations. Par prototypage, on entend une description des opérations par leur nom, leurs arguments et leur retour.

Les opérations sont divisées en plusieurs types :

• les constructeurs (permettent de créer un objet du type que l'on est en train de définir) ;
• les transformateurs (permettent de modifier les objets et leur contenu) ;
• les observateurs (fonction donnant des informations sur l'état de l'objet).

Exemple d'opération pour le type « TA : Pile » :

                   créer: -> Pile      

Notez que l'opération « créer » est un constructeur. En effet, cette fonction crée un objet de type pile. De plus, elle n'a pas besoin d'argument pour créer cette pile. Ceci est montré par l'absence d'indication à gauche de la flèche.

Pré-conditions

Le champ « Pré-conditions » contient les conditions à respecter sur les arguments d'une fonction pour que celle-ci puisse avoir un comportement normal. On peut parler ici d'ensemble de définitions de la fonction.

Axiomes

Le champ « Axiomes » contient une série d'axiomes pour décrire le comportement de chaque opération d'un type abstrait. Chaque axiome est une proposition logique vraie.

Exemple commenté : la Pile

On rappelle qu'une pile est une structure de données simple, respectant le principe LIFO (« Last In First Out »), c'est-à-dire que l'on accède toujours au dernier élément que l'on vient d'ajouter à cette structure.

On tient compte ici des opérations de base de la pile, ainsi que de l'opération « insérerFin » permettant d'insérer un élément à la fin de la pile (cette opération nous permettra de présenter la récursivité en type abstrait). Le symbole «   » signifie que l'opération est soumise à des pré-conditions.

On a ici un constructeur : créer ; trois transformateurs : empiler, reste et insérerFin ; et deux observateurs : sommet et estVide. L'opération « empiler » est considérée par certains comme un constructeur car on constate que toute pile est de la forme « empiler(p,e) » ou « créer() ».

Pré-conditions : p Pile défini(sommet(p)) estVide(p) défini(reste(p)) estVide(p)

Ces pré-conditions correspondent au fait que l'on ne peut pas « voir » le sommet ou prendre le reste d'une pile vide.

Axiomes : p Pile e, f Elément (P1) sommet(empiler(p,e)) = e (P2) reste(empiler(p,e)) = p (P3) estVide(créer()) = vrai (P3) estVide(empiler(p,e)) = faux (P4) insérerFin(créer(),e) = empiler(créer(),e) (P5) insérerFin(empiler(p,f),e) = empiler(insérerFin(p,e),f)