Ultrafiltre - Définition
La liste des auteurs de cet article est disponible ici.
Ultrafiltres triviaux et non-triviaux
Un ultrafiltre trivial (ou principal, ou fixé) est un filtre ayant un élément minimal. Les ultrafiltres triviaux sont donc de la forme Fa = {x | a ≤ x} pour un certain élément a de l'ensemble (partiellement ordonné) de base. Dans ce cas, a s'appelle l' élément principal de l' ultrafiltre. Dans le cas de filtres sur des ensembles, les éléments principaux sont exactement les singletons (les ensembles à un élément). Ainsi, un ultrafiltre trivial sur S est formé de tous les ensembles contenant un point donné de S. Les ultrafiltres sur des ensembles finis sont tous triviaux. Tout ultrafiltre non trivial est appelé un ultrafiltre libre (ou non-principal).
On peut montrer, en utilisant le lemme de Zorn que tout filtre (ou plus généralement tout sous-ensemble ayant la propriété d'intersection finie) est contenu dans un ultrafiltre, et par conséquent que des ultrafiltres libres existent, mais cette démonstration utilisant l'axiome de choix, il n'est pas possible de donner des exemples d'ultrafiltres non-triviaux, et il existe d'ailleurs des modèles de ZF n'en contenant pas. Cependant, si on admet l'axiome du choix, on peut montrer que presque tous les ultrafiltres sur un ensemble infini X sont libres, c'est-à-dire que le cardinal de l'ensemble des ultrafiltres libres est supérieur à celui de X, et donc à celui de l'ensemble des ultrafiltres triviaux.
Ordre sur les ultrafiltres
L'ordre de Rudin–Keisler est un préordre sur la classe des ultrafiltres défini de la manière suivante : si U est un ultrafiltre sur X, et V un ultrafiltre sur Y, alors
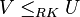
pour tout sous-ensemble C de Y.
Deux ultrafiltres U et V sont RK- équivalents,
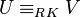

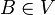
On démontre que
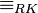
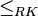
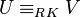
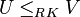
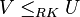
![C\in V\iff f^{-1}[C]\in U](https://static.techno-science.net/illustration/Definitions/autres/9/9cabace931645c46ba6a95ad3ef59e63_903b9447296ea4ced7534c635f86741f.png)

















































