Ultrafiltre - Définition

Complétude

Le degré de complétude d'un ultrafiltre U est le plus petit cardinal κ tel qu'il existe une famille de κ éléments de U dont l'intersection n'est pas dans U. Cette définition implique que le degré de complétude de tout ultrafiltre est au moins . Un ultrafiltre dont le degré de complétude est supérieur à — autrement dit, tel que l'intersection de toute famille dénombrable d'éléments de U est encore dans U — est dit dénombrablement complet ou encore σ-complet.

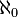
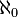
Le degré de complétude d'un ultrafiltre (non trivial) σ-complet est toujours un cardinal mesurable.

Applications

Les ultrafiltres (sur des ensembles) ont des applications en topologie, en particulier en relation avec l'étude de la compacité, et en théorie des modèles, pour la construction d'ultraproduits et d'ultrapuissances. Tout ultrafiltre sur un espace compact (séparé) est convergent, vers un point unique (et ce résultat caractérise les espaces compacts). De même, les ultrafiltres sur des ensembles partiellement ordonnés sont particulièrement utiles si l'ensemble est une algèbre de Boole, car alors ils coïncident avec les filtres premiers ; cette forme joue un rôle central dans le théorème de représentation de Stone.

L'ensemble G de tous les ultrafiltres sur un ordre partiel P peut être muni d'une structure topologique naturelle, qui est d'ailleurs étroitement reliée au théorème de représentation précédent : pour tout élément a de P, soit D_a = {U ∈ G | a ∈ U} ; alors, si P est une algèbre de Boole, l'ensemble de tous les D est une base d'une topologie compacte (séparée) sur G. En particulier, considérant les ultrafiltres sur un ensemble S (autrement dit, en prenant pour P l'ensemble des parties de S ordonné par inclusion), l'espace topologique correspondant est le compactifié de Stone–Čech de S muni de la topologie discrète.

La construction des ultraproduits en théorie des modèles utilise des ultrafiltres pour obtenir des extensions élémentaires de structures. Par exemple, la construction des nombres hyperréels commence par étendre le domaine du discours des réels à l'ensemble des suites de réels, considéré comme une extension des réels, identifiés aux suites constantes. Les opérations et les relations entre réels ne peuvent être directement être étendues aux suites, parce que, par exemple, les suites ne sont pas totalement ordonnées par l'ordre produit. On définit donc ces relations « modulo U » (où U est un ultrafiltre sur les entiers), c'est-à-dire, par exemple, qu'on pose (u_n) < (v_n) si l'ensemble des indices k tels que (u_k) < (v_k) appartient à U. D'après le théorème de Łoś, ceci préserve toutes les propriétés des réels exprimables dans une logique du premier ordre, et si U est non-trivial, l'extension ainsi obtenue contient de nouveaux objets (qui seront par exemple « infiniment grands », c'est-à-dire plus grands que tous les réels).

En théorie géométrique des groupes, on utilise des ultraproduits pour définir le cône asymptotique d'un groupe. Cette construction donne un sens rigoureux au fait de « considérer le groupe vu de l'infini », c'est-à-dire d'étudier la géométrie du groupe à grande échelle. Le cône asymptotique est un cas particulier de la notion d' ultralimite d'un espace métrique.

La preuve ontologique de Gödel (de l'existence de Dieu) utilise parmi ses axiomes une caractérisation de l'ensemble des « propriétés positives » qui en fait un ultrafiltre.