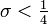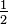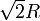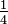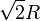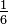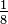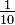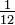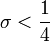Voûte de pont en maçonnerie - Définition

Introduction

La voûte est l’élément constitutif principal des ponts en maçonnerie, construits depuis la période romaine jusqu’à la fin du XIXe siècle, supportant toutes les charges appliquées sur l’ouvrage.

Une voûte en plein cintre

Terminologie

La voûte est délimitée par deux surfaces courbes :

• la surface extérieure appelée "extrados",
• la surface intérieure appelée intrados ou douelle.

Si l’on représente la projection d'une voûte sur un plan vertical, celle-ci est limitée par deux lignes, la ligne d'extrados et la ligne d'intrados. Cette dernière est généralement une courbe géométrique : arc de cercle, arc de parabole, etc .

La courbe naît sur les verticales limitant les culées.

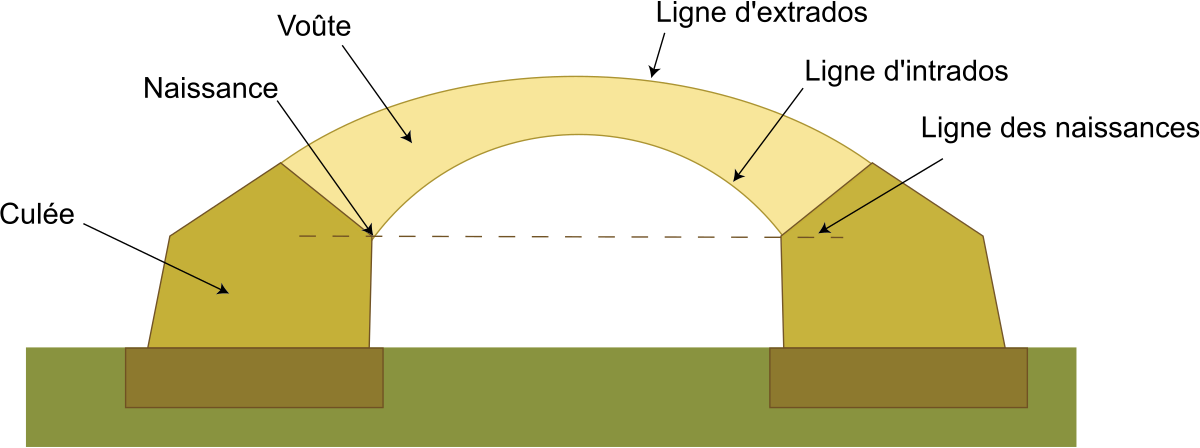
Les points d'intersection de la ligne d'intrados avec ces verticales s'appellent les naissances ou les reins. La distance qui sépare les culées s'appelle l'ouverture.

La ligne qui joint les naissances s'appelle ligne des naissances ou corde. Elle est presque toujours horizontale.

La distance verticale qui sépare la ligne d'intrados de la ligne des naissances, mesurée au milieu de celle-ci, s'appelle la flèche. Elle se représente par la lettre "f".

terminologie 1

terminologie 2

Caractéristiques géométriques d’une voûte

Caractéristiques d’une voûte

Une voûte se définit par :

• son ouverture,
• son surbaissement.

Si l'ouverture de la voûte est désignée par "2a" et la flèche par "f", le surbaissement de la voûte, désigné par la lettre σ, est le rapport flèche/ouverture soit :

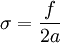
La ligne d'intrados

Connaissant l'ouverture et la flèche, on peut déterminer la ligne d'intrados.

S'il s'agit d'un arc de cercle, on rappelle à ce sujet la formule bien connue:

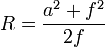
S'il s'agit d'un arc de parabole ou d’un arc d'ellipse on peut construire la ligne d'intrados soit d'une façon précise, à partir de l'équation de la courbe, soit d’une façon approchée en traçant l'arc de cercle qui s'en rapproche le plus.

L'épaisseur de la voute

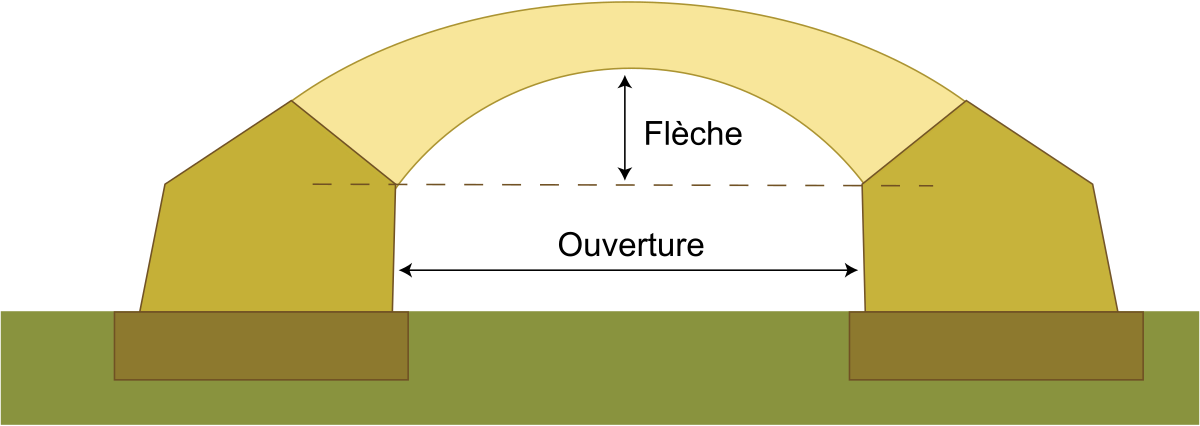
Il reste alors à déterminer l'épaisseur de la voûte. Celle-ci se définit à partir de certaines sections remarquables:

• celle du milieu ou section de clef,
• celles des naissances de la voûte, appelées sections des naissances,
• celles qui sont situées à mi-hauteur de la flèche, appelées sections aux reins.

Les caractéristiques d'un pont en maçonnerie ne peuvent se déterminer par les seules règles de la statique, mais seulement par approximations successives, à partir de dimensions choisies a priori que l'on vérifie; on dit que l'ouvrage est hyperstatique.

Puisque l'étude comporte un tâtonnement, on conçoit l'intérêt qui s'attache à choisir au départ, des dimensions aussi voisines que possible de celles qui seront en définitive retenues. On y parvient aisément grâce à la longue expérience que l'on a de ces ouvrages, qui a permis d'établir des formules empiriques donnant les épaisseurs à prévoir pour les sections remarquables des voûtes: clef, reins et naissances, ainsi que pour les culées et les piles.

Épaisseur à la clef

L'épaisseur à la clef (e₀) est donnée par les formules de Croizette-Desnoyers

Type de voûte	Surbaissement	Ponts-routes	Ponts-rails
Voûte en plein cintre		e0 = 0,15 + 0,15	e0 = 0,20 + 0,17
Voûte en arc de cercle		e0 = 0,15 + 0,15	e0 = 0,20 + 0,17
		e0 = 0,15 + 0,14	e0 = 0,20 + 0,16
		e0 = 0,15 + 0,13	e0 = 0,20 + 0,15
		e0 = 0,15 + 0,12	e0 = 0,20 + 0,14
		e0 = 0,15 + 0,11	e0 = 0,20 + 0,13
Voûte en arc d'ellipse		e0 = 0,15 + 0,15	e0 = 0,20 + 0,17

Épaisseur aux reins

Paul Séjourné conseille la formule :

avec pour λ les valeurs suivantes :

Type de voûte	Valeur de λ	Commentaires
Voûte en plein cintre	λ = 2	Cette valeur est un peu forte pour les voûtes de faible ouverture, inférieure à 8 m
Voûte en arc d'ellipse	λ = 1 + 2σ	σ étant le surbaissement
Voûte en arc de cercle	λ = 2	pour
	λ = 1 + 12σ2	pour

Épaisseur aux naissances

Pour les voûtes peu surbaissées (), il n'y a généralement pas lieu de connaître l'épaisseur aux naissances qui se confond pratiquement avec les reins, les culées commençant à partir de ceux-ci.

Pour les voûtes surbaissées ( ), on utilisera la formule suivante donnée par Paul Séjourné :