Ensemble - Définition

Introduction

En théorie des ensembles, un ensemble désigne intuitivement une collection d’objets (les éléments de l'ensemble), « une multitude qui peut être comprise comme un tout », comme l'énonçait son principal initiateur, le mathématicien Georg Cantor : (de) « Unter einer 'Menge' verstehen wir jede Zusammenfassung M von bestimmten wohlunterscheidbaren Objekten M unserer Anschauung oder unseres Denkens (welche die 'Elemente' von M genannt werden) zu einem Ganzen » : « Par ensemble, nous entendons toute collection M d'objets m de notre intuition ou de notre pensée, définis et distincts, ces objets étant appelés les éléments de M ». Ceci était particulièrement novateur, s'agissant d'ensembles éventuellement infinis (ce sont ces derniers qui intéressaient Cantor).

Ce qui est en jeu au premier chef dans la notion d'ensemble, c'est la relation d’appartenance : un élément appartient à un ensemble. Ce sont les propriétés de cette relation que Zermelo, puis d'autres, ont axiomatisé en théorie des ensembles. Il est assez remarquable que l'on puisse s'en contenter pour une théorie qui peut potentiellement formaliser les mathématiques. Mais ce n'était pas l'intention de Cantor, et il n'avait pas non plus axiomatisé sa théorie.

L'objet de cet article est de donner une approche intuitive de la notion d'ensemble, telle qu'elle est indiquée dans l'article théorie naïve des ensembles.

Ensembles, éléments et appartenance

Un ensemble peut être vu comme une sorte de sac virtuel entourant ses éléments, ce que modélisent bien les diagrammes de Venn. Souvent (ce n'est pas toujours possible), on essaye de le distinguer typographiquement de ses éléments, par exemple en utilisant une lettre latine majuscule, par exemple « E » ou « A », pour représenter l'ensemble, et des minuscules, telles que « x » ou « n », pour ses éléments.

Les éléments peuvent être de n’importe quelle nature : nombres, points géométriques, droites, fonctions, autres ensembles... On donne donc volontiers des exemples d'ensembles en dehors du monde mathématique. Par exemple : lundi est un élément de l’ensemble des jours de la semaine ; une bibliothèque est un ensemble de livres, etc.

Un même objet peut être élément de plusieurs ensembles : 4 est un élément de l'ensemble des nombres entiers, ainsi que de l’ensemble des nombres pairs (forcément entiers). Ces deux derniers ensembles sont infinis, ils ont une infinité d’éléments.

L'appartenance d'un élément, noté par exemple x, à un ensemble, noté par exemple A, s’écrit : .

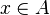
Cet énoncé peut se lire :

• « x appartient à A »,
• « x est élément de A »,
• « x est dans A »,
• « A a pour élément x »,
• « A possède x »,
• ou parfois « A contient x » (il y a ambiguïté cependant dans ce dernier cas, A contient x peut signifier que x est un sous-ensemble de A, c’est-à-dire que x est un ensemble et que tous ses éléments appartiennent à A, ce qui est très différent de « x appartient à A »).

Le symbole « ∈ », dérive de la lettre grecque ε (epsilon) introduite par Giuseppe Peano dès 1889. Pour Peano « x ε A » se lit « x est un A », par exemple « x ε N » se lit « x est un entier ». Le ε renvoie à l'initiale du mot « est » (en latin, langue de l'article de Peano de 1889 !), en français, ou en italien (« è »). Bertrand Russell reprend les notations de Peano en 1903 dans les Principles of Mathematics, ouvrage qui va participer à leur diffusion, et où est utilisée la forme arrondie vieillie du epsilon : « ϵ », en usage dans l'édition mathématique anglo-saxonne.

Comme souvent pour les relations, on barre ce symbole pour indiquer sa négation, la non-appartenance d’un objet à un ensemble :

«   » signifie « z n’appartient pas à A ».