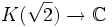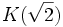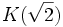Automorphisme de corps non continu de C - Définition
Le seul automorphisme de corps de



Soit E l'ensemble des sous-corps de



La maximalité de K permet de montrer que l'extension
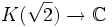

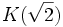

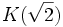

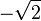




Le seul automorphisme de corps de



Soit E l'ensemble des sous-corps de



La maximalité de K permet de montrer que l'extension