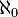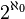Puissance du continu - Définition
En mathématiques, on dit d'un ensemble qu'il a la puissance du continu si son cardinal est le même que celui du corps des réels, c'est-à-dire
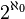
On montre qu'un ensemble E a la puissance du continu s'il existe une bijection entre E et

Une grande question des mathématiques a été de savoir s'il existait des ensembles dont le cardinal est plus grand que celui du dénombrable (le cardinal de