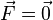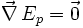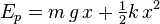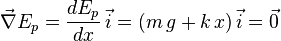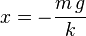Énergie potentielle mécanique - Définition

L'énergie potentielle mécanique est l'énergie que possède un système du fait de sa position :

• Position : énergie potentielle de pesanteur
• Forme : énergie potentielle élastique

L'énergie potentielle mécanique est en réserve, elle se manifeste quand elle se transforme en énergie cinétique. Elle est intrinsèquement liée à la notion de force conservative.

L'énergie potentielle est définie à une constante additive près. Celle-ci n'a aucune influence sur les résultats puisque l'énergie potentielle est utilisée dans des opérations de dérivation (calcul d'une force conservative) ou de variation (calcul d'un travail). Ces deux opérations faisant disparaître la constante, le choix de cette dernière est donc purement arbitraire et sa détermination se fait généralement de façon à simplifier les calculs.

Condition d'équilibre

Quand un système possède une énergie potentielle E_p, il existe une force conservative F définie par la relation suivante :

(où est l’opérateur gradient)

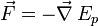
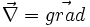
Dans le cas où le système est soumis à cette seule force, on sait d'après les lois de Newton que le système est en équilibre si

On en déduit une condition d'équilibre pour un système possédant une énergie potentielle :

Le système est donc en équilibre quand son énergie potentielle est maximale ou minimale.

Exemple

Considérons un système composé d'une masse m soumise à l'action de la gravité et suspendue à un ressort de raideur k. Dans ce cas, l'énergie potentielle du système est égale à la somme d'une énergie potentielle de pesanteur m g x et d'une énergie potentielle élastique k x²/2.

Dans le repère la condition d'équilibre donne alors :

dont on déduit la condition d'équilibre :

Comme on peut le voir sur le graphique plus haut, cette position d'équilibre correspond au minimum de l'énergie potentielle du système.