Étalonnage de caméra - Définition
En traitement d'image, l'opération d'étalonnage d'une caméra revient à modéliser le processus de formation des images, c'est-à-dire trouver la relation entre les coordonnées spatiales d'un point de l'espace avec le point associé dans l'image prise par la caméra.
Modélisation
Plusieurs modèles décrivant le processus de formation des images existent. Le plus simple est le modèle du sténopé ou modèle pin-hole dans la littérature anglo-saxonne. Ce dernier est couramment utilisé en traitement d'image.
Notations
Il convient de préciser les repères orthonormés dans lesquels nous allons travailler pour modéliser le fonctionnement de la caméra :
Les repères associés sont :
-
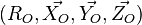
-
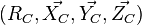
-
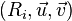
Un plan supplémentaire n'a pas été représenté ici qui est dans le repère associé à la caméra. C'est le plan image qui est à une distance f de C suivant la direction donnée par
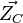
Le modèle du sténopé
Appelé aussi modèle pin-hole dans la littérature anglo-saxonne, il s'agit d'une modélisation simple et linéaire du processus de formation des images au sein d'une caméra. Ce modèle suppose que le système optique de la caméra, c'est-à-dire sa lentille respecte les conditions de Gauss. Si l'on utilise la notation matricielle des coordonnées homogènes, il est possible de décrire de manière simple ce processus. Il suffit d'exprimer les relations de passage du repère monde au repère caméra, d'exprimer la projection du repère caméra dans le plan image et d'appliquer la transformation affine qui conduit aux coordonnées de l'image. La relation est la suivante pour un point M de coordonnées (X,Y,Z,1) dans l'espace (repère monde) et dont l'image est de coordonnées (su,sv,s) dans le plan image :
![\left( \begin{matrix} su \\ sv \\ s \\ \end{matrix} \right) = \left[ \begin{matrix} k_u & s_{uv} & c_u \\ 0 & k_v & c_v \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} & & & t_x \\ & R_{3\times3} & & t_y \\ & & & t_z \\ 0&0&0&1 \end{matrix} \right] \left( \begin{matrix} X \\ Y \\ Z \\ 1\\ \end{matrix} \right)](https://static.techno-science.net/illustration/Definitions/autres/3/35c0c02fc82afcad85534f80f98e4fb1_407336c234d728e26a02ddb0dd32be1d.png)
Les paramètres employés dans ce modèle sont usuellement divisés en deux catégories : les paramètres intrinsèques qui sont internes à la caméra, et les paramètres extrinsèques qui peuvent varier suivant la position de la caméra dans l'espace de travail. Parmi les paramètres intrinsèques nous comptons :
- f : la distance focale,
- ku et kv : les facteurs d'agrandissement de l'image,
- cu et cv : les coordonnées de la projection du centre optique de la caméra sur le plan image,
- suv : qui traduit la non-orthogonalité potentielle des lignes et des colonnes de cellules électroniques photosensibles qui composent le capteur de la caméra. La plupart du temps, ce paramètre est négligé et prend donc une valeur nulle.
Les paramètres extrinsèques sont :
-
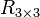
- tx,ty et tz : qui sont les composantes du vecteur de translation permettant de passer du repère lié à l'espace de travail au repère lié à la caméra.
Au total, cela fait 18 paramètres à estimer (la matrice de rotation en contient 9).
Étalonner la caméra consiste à déterminer la valeur numérique des paramètres de ce modèle. Il est toutefois possible de les regrouper de manière différente, suivant la forme sous laquelle ce modèle doit ensuite être exploité. Ceci conduit à différentes variantes possibles du modèle.
Variantes du modèle du sténopé
Certaines variantes du modèle du sténopé regroupent les paramètres intrinsèques de la manière suivante :
![\left[ \begin{matrix} \alpha_u & S_{uv} & u_0 & 0 \\ 0 & \alpha_v & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix} \right] = \left[ \begin{matrix} k_u & s_{uv} & c_u \\ 0 & k_v & c_v \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/c/cd06a4cec2d780fe8cf3cdf18a77d628_79283158bb6d800190cccd9f6268e27d.png)
Sachant que l'expression f.suv est souvent considérée comme étant nulle, nous obtenons un nouveau jeu simplifié de paramètres intrinsèques :
- αu et αv (parfois aussi appelés fx et fy dans la littérature) qui correspondent à la distance focale exprimée en largeurs et en hauteurs de pixels (ces derniers ne sont pas nécessairement carrés),
- u0 et v0 qui sont les coordonnées de la projection du centre optique de la caméra sur le plan image.
Cette variante contient 17 paramètres à estimer. Elle présente l'avantage de séparer en deux matrices les paramètres intrinsèques et extrinsèques et donc d'isoler ces derniers qui changent de valeur à chaque fois que la caméra est déplacée dans l'espace de travail.
Une autre variante consiste à n'utiliser qu'une matrice globale de paramètres à estimer :
![\left[ \begin{matrix} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \end{matrix} \right] = \left[ \begin{matrix} k_u & s_{uv} & c_u \\ 0 & k_v & c_v \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} & & & t_x \\ & R_{3\times3} & & t_y \\ & & & t_z \\ 0&0&0&1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/8/8bb2754f800e256d224dc4270c2215a7_cf2daa4aa888d7d6f9f69cee88d855f0.png)
Cette dernière ne présente que 12 paramètres à estimer mais il est nécessaire de les réestimer à chaque fois que la caméra est déplacée.
Toutefois, dans le cas des objectifs grand-angle, les conditions optiques de Gauss ne sont plus respectées, ce qui induit des déformations optiques dans l'image finale dont il faut alors tenir compte.

















































