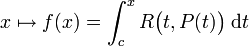Intégrale elliptique - Définition

Une fonction intégrale elliptique est une fonction f de la forme :

où R est une fonction rationnelle à deux variables, P est la racine carrée d'une fonction polynomiale de degré 3 ou 4 avec des racines simples et c est une constante.

Les intégrales elliptiques " complètes " de première espèce peuvent être calculées par des considérations géométriques.

Les intégrales elliptiques sont les applications réciproques des fonctions elliptiques.