Fonction de Kummer - Définition
En mathématiques, il existe plusieurs fonctions connues sous le nom fonction de Kummer. L'une d'elle est connue comme la fonction hypergéométrique confluente de Kummer et de E. T. Whittaker. Une autre, définie ci-dessous, est reliée à la fonction polylogarithme. Les deux ont été nommées en l'honneur du mathématicien Ernst Kummer.
La fonction de Kummer est définie par
-
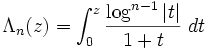
La formule de duplication est
-
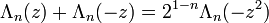
Comparons celle-ci à la formule de duplication du polylogarithme :
-
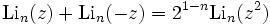
Un lien explicite vers le polylogarithme est donné par
-
![\operatorname{Li}_n(z)=\operatorname{Li}_n(1)\;\;+\;\; \sum_{k=1}^{n-1} (-1)^{k-1} \;\frac{\log^k |z|} {k!} \;\operatorname{Li}_{n-k} (z) \;\;+\;\; \frac{(-1)^{n-1}}{(n-1)!} \;\left[ \Lambda_n(-1) - \Lambda_n(-z) \right]](https://static.techno-science.net/illustration/Definitions/autres/6/666645a8dd936e2809f50ba03164fbae_0046cd3f2cd7da3c8f682ba0e94528e2.png)
Publication
Leonard Lewin (Ed.). Structural Properties of Polylogarithms (1991) Providence, RI: American Mathematical Society, Providence RI. ISBN 0-8218-4532-2

















































