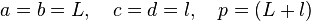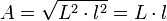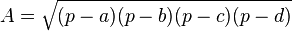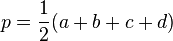En géométrie euclidienne, la formule de Brahmagupta, trouvée par Brahmagupta, est une généralisation de le Formule de Héron à l'aire d'un quadrilatère convexe dont les sommets se situent sur un même cercle, en ne connaissant que la longueur (La longueur d’un objet est la distance entre ses deux extrémités les plus éloignées. Lorsque l’objet est filiforme ou en forme de lacet, sa longueur est celle de...) de ses côtés:

et

est le demi-périmètre du quadrilatère (En géométrie plane, un quadrilatère est un polygone à 4 côtés.), a, b, c et d sont les longueurs des côtés du quadrilatère et A l'aire du quadrilatère.

Démonstration (En mathématiques, une démonstration permet d'établir une proposition à partir de propositions initiales, ou précédemment...)

Cas particuliers

• Le carré : et
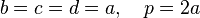
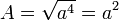
• Le rectangle : et