Quadrilatère - Définition

Introduction

QUADRILATÈRES
┌─────────────┼─────────────┐
concave		convexe		croisé
┌─────────────┼─────────────┐
à cercle circonscrit		trapèze		tangentiel
| ┌───────────┤				|
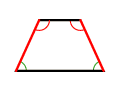
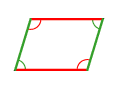
trapèze isocèle		parallélogramme		cerf-volant
└─────┬─────┘			└─────┬─────┘
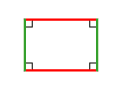
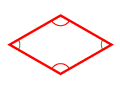
rectangle			losange
└──────────┬─────────┘
carré

En géométrie plane, un quadrilatère (parfois appelé tétrapleure ou tétragone) est un polygone à quatre côtés. Les trapèzes, parallélogrammes, losanges, rectangles, carrés et cerfs-volant sont des quadrilatères particuliers.

Étymologie

Le mot quadrilatère provient du latin : quatuor, quatre et latus, lateris, côté. Le mot équivalent d'origine grecque est tétrapleure (de τέττερα / tettera, quatre et πλευρά / pleura, côté) ou tétragone (de γωνία / gônia, angle). Le mot tétragone était employé par Gerbert d'Aurillac au X^e siècle et par Oresme au XIV^e siècle. Le terme quadrilatère est introduit en 1554 par Peletier. Certains auteurs latins employaient le mot « quadrangle » (Alcuin, VIII^e siècle) ou « helmuariphe », terme d'origine arabe (Campanus, XIII^e siècle, et d'autres à la Renaissance). Pour les Grecs, un quadrilatère avec un angle rentrant s'appelait un « koïlogone » (de κοιλοσ / koïlos, creux), et certains appelaient « trapèze » un quadrilatère dont tous les côtés sont inégaux. « Tétragone » est employé par Euclide dans Les Éléments pour désigner le carré.

Quadrilatère convexe

En géométrie élémentaire, une grande place est accordée aux quadrilatères convexes.

Un quadrilatère est convexe si et seulement si, quel que soit le côté que l'on choisit, le quadrilatère est entièrement inclus dans un demi-plan dont la frontière porte ce côté. Cette caractérisation est générale à tout polygone convexe. Dans le cas particulier du quadrilatère, il existe aussi une autre caractérisation : un quadrilatère est convexe si et seulement si les diagonales forment des segments sécants.

Quand un quadrilatère est convexe, une droite du plan ne passant pas par un sommet ne peut pas rencontrer plus de deux côtés du quadrilatère.

Somme des angles : la somme des angles d'un quadrilatère convexe vaut 360 ° mais cette propriété n'est plus vraie pour un quadrilatère concave.

Aire : l'aire d'un quadrilatère convexe est égale au demi-produit des diagonales multiplié par le sinus de l'angle qu'elles forment (l'angle utilisé étant le plus petit des deux angles formés par les droites).

L'intérieur d'un quadrilatère convexe ABCD est alors défini comme l'intersection des demi-plans délimités par (AB), par (BC), par (CD) et par (DA) et contenant respectivement chacun les points C, D, A et B. Il est alors possible, dans un plan muni d'un repère cartésien, de définir l'intérieur d'un quadrilatère en comparant des signes : le point P(x,y) est intérieur au quadrilatère convexe ABCD si et seulement si les quatre conditions suivantes sont vérifiées :

(y_B − y_A)x − (x_B − x_A)y − x_A.y_B + x_B.y_A a même signe que (y_B − y_A)x_C − (x_B − x_A)y_C − x_A.y_B + x_B.y_A

(y_C − y_B)x − (x_C − x_B)y − x_B.y_C + x_C.y_B a même signe que (y_C − y_B)x_D − (x_C − x_B)y_D − x_B.y_C + x_C.y_B

(y_D − y_C)x − (x_D − x_C)y − x_C.y_D + x_D.y_C a même signe que (y_D − y_C)x_A − (x_D − x_C)y_A − x_C.y_D + x_D.y_C

(y_A − y_D)x − (x_A − x_D)y − x_D.y_A + x_A.y_D a même signe que (y_A − y_D)x_B − (x_A − x_D)y_B − x_A.y_A + x_A.y_D