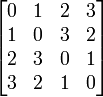Carré latin - Définition
Un carré latin est un tableau carré de n lignes et n colonnes remplies de n éléments distincts dont chaque ligne et chaque colonne ne contient qu'un seul exemplaire. La plupart du temps, les n éléments utilisés sont les entiers compris entre 0 et n-1, même si cela n'a aucune importance.
Voici un exemple de carré latin :
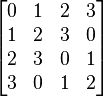
Un peu de mathématiques
En permutant deux lignes ou deux colonnes d'un carré latin, on obtient encore un carré latin.
À une bijection près sur les n éléments, et à des permutations près sur les lignes et les colonnes, il n'existe qu'un seul carré latin d'ordre 3
| Carré latin correspondant au groupe cyclique (Z/3Z; +) |
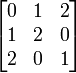
En revanche il existe deux carrés latins d'ordre 4 (si l'on ne tient pas compte des permutations ou des éventuelles bijections sur les n éléments) :
| Carré latin correspondant au groupe cyclique (Z/4Z; +) |
|
| Carré latin correspondant au groupe de Klein |
|
Les carrés latins sont les tables d'opérations de quasigroupes finis et ont un lien étroit avec les carrés magiques.