Matrice échelonnée - Définition

Une matrice est dite échelonnée, si le nombre de zéros précédant la première valeur non nulle d'une ligne augmente ligne par ligne jusqu'à ce qu'il ne reste plus que des zéros.

Voici un exemple de matrice échelonnée (les désignent des coefficients arbitraires, les des pivots, coefficients non nuls)

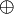
Un exemple de matrice échelonnée réduite ou matrice canonique en lignes (les pivots valent 1 et les autres coefficients dans les colonnes des pivots sont nuls)