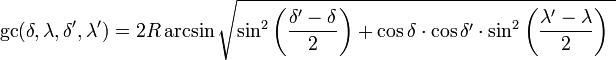Distance du grand cercle - Définition
La distance du grand cercle plus généralement appelée distance orthodromique ou simplement orthodromie est la plus petite distance entre deux points sur une sphère. Comme la Terre est approximativement une sphère, la distance du grand cercle est souvent utilisée pour trouver la distance entre deux coordonnées (en connaissant leur longitude et leur latitude) sur une carte.
Définitions
-
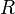
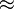
-
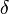
-

La formule
Voir Orthodromie