Conservation des masses - Définition

En mécanique des fluides, le principe de conservation de la masse peut s'exprimer sous plusieurs formes différentes : locale conservative (dérivée en temps normale), locale non conservative (la dérivée en temps suit la particule dans son mouvement), ou intégrale. Suivant les problèmes posés, c'est l'une ou l'autre de ces équations qui pourra être retenue, toutes étant équivalentes.

On note ici :

 : masse volumique du fluide

 : vitesse du fluide

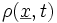
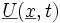
Forme locale conservative

C'est la forme la plus couramment utilisée ; elle est bien adaptée aux problèmes stationnaires.

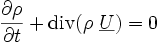
Forme locale non conservative

Forme intégrale

C'est une formule très générale, qui permet l'étude de tout un volume de fluide Ω(t). Elle exprime que la masse du fluide dans un volume bien délimité et qui suit le mouvement du liquide est constante.

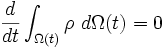
Conditions de saut

Lorsque le composé étudié est constitué de deux fluides différents non miscibles séparés par une interface Σ(t) se déplaçant à une vitesse de propagation locale , la conservation de la masse s'exprime par la relation suivante :

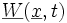
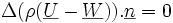
où Δ(b) = b₂ − b₁ si b₁ et b₂ sont les valeurs respectives de la grandeur b dans les deux fluides 1 et 2 et est le vecteur normal à Σ(t) orienté du fluide 1 vers le fluide 2.