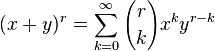Binôme généralisé - Définition
La formule du binôme généralisé permet de développer une puissance réelle ou complexe d'une somme de deux termes sous forme d'une somme de série et généralise la formule du binôme de Newton.
Nous avons pour tous réels ou complexes r, x et y (y ≠ 0) tels que |x/y|<1,
où 
est un coefficient binomial.
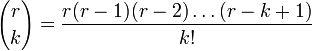
(qui dans le cas où k = 0 est un produit vide et donc égal à 1, et dans le cas où k = 1 est égal à r, les facteurs supplémentaires ( r – 1), etc., ne figurant pas dans ce cas).
La série correspondante est convergente et l'égalité reste valable toutes les fois que les nombres réels ou complexes x et y sont dans un rapport de module strictement inférieur à 1.
La somme d'une série géométrique est un cas particulier de la formule obtenu en prenant y = 1 et r = -1.
La formule reste également valable pour des éléments x et y d'une algèbre de Banach, qui commutent (xy = yx ), tels que y soit inversible et ||x.y-1||< 1.