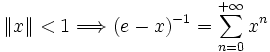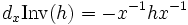Algèbre de Banach - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, l'algèbre de Banach est une des structures fondamentales de l'analyse fonctionnelle, portant le nom du mathématicien polonais Stefan Banach (1892-1945).
Définition
Définition — Une algèbre de Banach

Suivant les auteurs, la structure d'algèbre exige ou non la présence d'un élément unité. Les termes algèbre unitaire et algèbre non unitaire permettent de différencier les structures. En analyse fonctionnelle, une algèbre de Banach est dite unitaire lorsqu'il existe un élément neutre, nécessairement unique, e, et que la norme de e est 1.
On parle en outre d'algèbre de Banach commutative quand la loi produit est commutative.
Exemples
- L'ensemble des nombres réels muni de la valeur absolue, de la somme et du produit est une algèbre de Banach réelle et unitaire. De même, l'ensemble des nombres complexes, muni du module, de la somme et du produit est une algèbre de Banach complexe et unitaire. Ces exemples sont fondamentaux.
- Si H est un espace vectoriel réel ou complexe normé complet, l'algèbre des opérateurs bornés (c'est-à-dire des endomorphismes réels ou complexes continus) de H est une algèbre de Banach réelle ou complexe (unitaire) pour la norme d'opérateurs correspondante, la somme et la composition d'opérateurs. Delà en découle la théorie de la représentation des algèbres de Banach.
- L'exemple (précédent) concerne notamment les algèbres d'endomorphismes en dimension finie : en particulier,
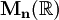
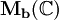
- L'espace L1 des fonctions intégrables sur

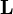
- Plus généralement, dans la théorie de Lebesgue, l'espace des fonctions intégrables sur un espace mesuré est un espace de Banach. La complétude demande une démonstration qui s'appuie sur un rapprochement entre convergence L1 et convergence presque partout.
Propriétés des algèbres unitaires
Soit
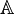
Propriétés de l'application de passage à l'inverse
Comme dans toute algèbre, les éléments inversibles de A forment un groupe. Tout élément x appartenant à la boule ouverte de centre e et de rayon 1 en fait partie, et son inverse peut être exprimé comme somme de la série géométrique de raison x.
Le groupe G des éléments inversibles d'une algèbre de Banach est un ouvert.
Soit un élément inversible a de A et
- r = | | a − 1 | | − 1.
Soit x un élément de
- | | a − 1(a − x) | | < 1
donc e − a − 1(a − x) est inversible. L'élément a étant inversible, le produit
- a(e − a − 1(a − x)) = x
L'application de passage à l'inverse est un homéomorphisme de G sur G, ce qui confère à G une structure de groupe topologique. Il s'agit même d'une application différentiable, la différentielle au point x étant donnée par la formule
L'hypothèse de complétude est essentielle et ces résultats tombent en défaut dans les algèbre normée non complète. Par exemple considérons l'algèbre des polynômes à coefficients réels
![\mathbb{R}[X]](https://static.techno-science.net/illustration/Definitions/autres/5/5e11093b37fd30fbaa413f6bdf9647c4_bf95e896a54c240387ad57c91bfa743b.png)
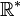

![\mathbb{R}[X]](https://static.techno-science.net/illustration/Definitions/autres/5/5e11093b37fd30fbaa413f6bdf9647c4_bf95e896a54c240387ad57c91bfa743b.png)
![\mathbb{R}[X]](https://static.techno-science.net/illustration/Definitions/autres/5/5e11093b37fd30fbaa413f6bdf9647c4_bf95e896a54c240387ad57c91bfa743b.png)

Idéaux et algèbre quotient
Les idéaux maximaux d'une algèbre de Banach sont fermés.
Une algèbre de Banach complexe dont tout élément non nul est inversible est isomorphe, par l'intermédiaire d'une isométrie, au corps des nombres complexes (théorème de Gelfand-Mazur); en particulier, les idéaux maximaux des algèbres de Banach complexes sont des hyperplans fermés. La commutativité est une conséquence du théorème.