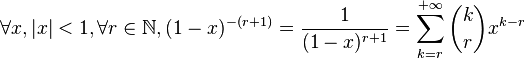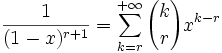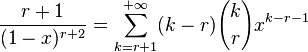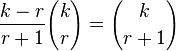Formule du binôme négatif - Définition
La formule du binôme négatif permet de développer une puissance entière strictement négative d'une somme de deux termes, et apparaît comme un cas particulier de la formule du binôme généralisé.
Énoncé
Nous avons :
où

Démonstration
La formule se montre par récurrence sur r en utilisant les règles de dérivation des séries entières.
Pour r = 0, on reconnaît
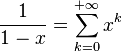
Supposons la formule vraie au rang r :
et dérivons-la. On obtient :
ce qui donne le résultat voulu au rang suivant compte tenu du fait que
Voyez également
- Le théorème du binôme généralisé
- La formule du binôme de Newton
- Les coefficients binomiaux
- Les séries