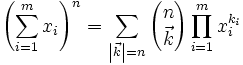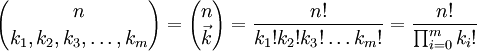Formule du multinôme de Newton - Définition
En mathématiques, la formule du multinôme de Newton est une relation donnant le développement d'une puissance entière n d'une somme d'un nombre fini m de termes sous forme d'une somme de produits de puissances de ces termes affectés de coefficients. Nous avons pour tous entiers naturels m et n, et pour tous réels ou complexes
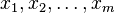
-
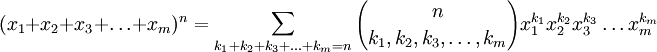
La somme porte sur toutes les combinaisons d'indices entiers naturels
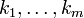
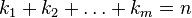
Une écriture équivalente mais bien plus concise consiste à sommer sur tous les multi-indices
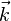
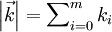
Les nombres
sont appelés les coefficients multinomiaux.
La formule du binôme s'obtient comme cas particulier de la formule du multinôme, pour m = 2 ; et dans ce cas les coefficients multinomiaux sont les coefficients binomiaux.
Exemples
Voyez également
- La formule du binôme de Newton
- La formule du trinôme de Newton
- Le coefficient binomial