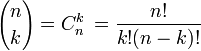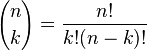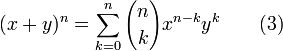Coefficient binomial - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Établissement de la formule - Utilisation des coefficients binomiaux - Définition algébrique des coefficients binomiaux d'entiers - Généralisations - Diviseurs et coefficients binomiaux - Formules faisant intervenir les coefficients binomiaux

Introduction

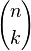
En mathématiques, (algèbre et dénombrement) les coefficients binomiaux, définis pour tout entier naturel n et tout entier naturel k inférieur ou égal à n, donnent le nombre de sous-ensembles différents à k éléments que l'on peut former à partir d'un ensemble contenant n éléments. On les note ${n \choose k}$ (lu « k parmi n » ) ou $C_n^k\,$ (lu « combinaison de k parmi n »), la première notation étant préconisée en France pour l'enseignement des mathématiques en terminale scientifique. Cette quantité s'exprime à l'aide de la fonction factorielle :

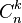
Les coefficients binomiaux interviennent dans de nombreux domaines des mathématiques : développement du binôme, dénombrement, développement en série, lois de probabilités.

On peut les généraliser, sous certaines conditions, aux nombres complexes.

Établissement de la formule

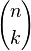
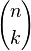
L'expression de ${n \choose k}$ se détermine en utilisant les arrangements. On calcule le nombre d'arrangements ou de listes ordonnées à k éléments pris dans un ensemble en contenant n de deux façons différentes. La confrontation des deux calculs donne l'expression algébrique de ${n \choose k}$

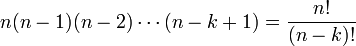
Une liste ordonnée de k éléments pris parmi n peut être constituée en choisissant le premier élément parmi n, (n choix possibles), puis le deuxième élément parmi n -1 (n -1 choix possibles) , etc. le dernier élément étant choisi parmi n - k+1 éléments. Il existe donc $n(n-1)(n-2) \cdots (n-k+1) = \dfrac{n!}{(n-k)!}$ listes ordonnées de k éléments pris parmi n.
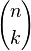
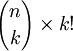
Mais on peut aussi choisir d'abord le sous-ensemble des k éléments parmi n ( ${n \choose k}$ choix possibles) puis ordonner l'ensemble pour constituer une liste ( $k!$ ordres possibles). Il existe donc ${n \choose k} \times k!$ listes ordonnées de k éléments pris parmi n.

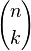
En confrontant ces deux expressions, on obtient l'expression de ${n \choose k}$ :

Utilisation des coefficients binomiaux

Développement du binôme de Newton

Ces nombres sont les coefficients qui apparaissent en développant la puissance n^ieme de x + y :

Par exemple, en regardant la cinquième ligne du triangle de Pascal, on obtient immédiatement que :

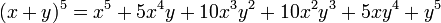
Combinatoire et statistique

Les coefficients binomiaux sont importants en combinatoire, parce qu'ils fournissent des formules utilisées dans des problèmes fréquents de dénombrement :

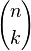
Le nombre de parties à k éléments dans un ensemble à n éléments est égal à ${n \choose k}$ . C'est également le nombre de listes de longueur n, constituées de 1 et de 0, et ayant k fois l'élément 1 et n-k l'élément 0. Ces parties ou ces listes sont appelées des k-combinaisons sans répétition.
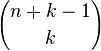
Le nombre de suites de n entiers naturels dont la somme vaut k est égale à ${n+k-1 \choose k}$ . C'est aussi le nombre de façons de choisir k éléments d'un ensemble à n éléments si les répétitions sont permises (nombre de combinaisons avec répétition).
En probabilité et statistique, les coefficients de binôme apparaissent dans la définition de la loi binomiale .
Ils interviennent dans la définition des polynômes de Bernstein et dans l'équation paramétrique d'une courbe de Bézier.
D'un point de vue plus intuitif, ce nombre permet de savoir combien de tirages de k éléments parmi n différents on peut réaliser. Exemple: les quatre as d'un jeu de cartes sont face contre table, on veut savoir combien de possibilités de jeu il existe si l'on prend simultanément deux cartes au hasard. Si l'on suit la formule il y en a six.