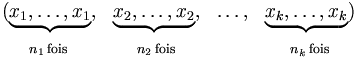Permutation avec répétition - Définition

En mathématiques, lorsque nous permutons n objets partiellement discernables et rangés dans un certain ordre, nous retrouvons dans certains cas la même disposition. Considérons n objets dont k seulement sont distincts (k ≤ n) placés dans un n-uplet, et supposons que chacun d'entre eux apparaisse respectivement n₁ fois, n₂ fois, ..., n_k fois avec n₁+n₂+...+n_k=n. Quand des éléments identiques de ce n-uplet sont permutés, nous obtenons le même n-uplet.
Par exemple, si nous voulons déterminer toutes les anagrammes du mot MATHÉMATIQUE, nous voyons qu'en échangeant les deux lettres A, le mot reste identique, et par contre en transposant les lettres É et E nous obtenons un mot différent.

Définition :

Soit E un ensemble fini de cardinal k (k ∈ ?^∗), E={x₁, x₂, ..., x_k}. Soient n un entier tel que k ? n et n₁, n₂, ..., n_k des entiers naturels tels que

n₁+n₂ + ... + n_k=n.

Une permutation de n éléments de E avec n₁, n₂, ..., n_k répétitions, est un n-uplet d'éléments de E dans lequel chacun des éléments x₁, x₂, ..., x_k de E apparaît n₁, n₂, ..., n_k fois.

Exemple :

Le n-uplet

est une permutation avec répétition particulière.

Théorème :

Le nombre p(n₁, n₂, ..., n_k) de permutations de n éléments avec n₁, n₂, ..., n_k répétitions est

.

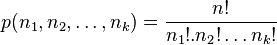
Ce nombre se note habituellement .

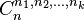
Démonstration :

Pour construire un n-uplet correspondant à une combinaison contenant n₁ fois x₁, n₂ fois x₂, ..., n_k fois x_k, il suffit

• de choisir les n₁ emplacements des x₁, parmi n₁ + n₂ + ... +n_k places disponibles,
• de choisir les n₂ emplacements des x₂, parmi les n₂ + ... +n_k places restantes,
• etc.
• de choisir les n_k emplacements des x_k, parmi les n_k places restantes.

Au total, il y a

.

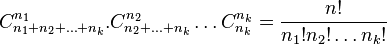
Application

Le développement de ce produit de facteurs est une somme de produits qui peuvent être représentés par un n-uplet d'éléments x₁, x₂, ..., x_k dans lequel pour tout 1 ? i ? n, un terme du i-ième facteur se trouve à la ième place.

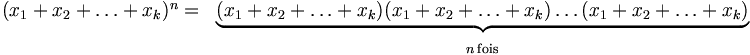
Pour tout 1 ? i ? k, notons n_i le nombre de fois où x_i apparaît dans un tel n-uplet. Nous avons

n₁ + n₂ + ... + n_k=n.

Le produit correspondant à un tel n-uplet est de la forme

.

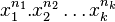
Étant donnés les entiers naturels n₁, n₂ , ... , n_k tels que n₁ + n₂ + ... + n_k=n, le nombre de termes de la forme est le nombre de permutations de n éléments avec n₁, n₂ , ... , n_k répétitions.

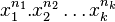
Ainsi

.

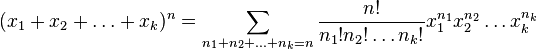
Voyez également

• Permutation
• coefficient multinomial
• Formule du multinôme