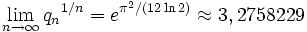Constante de Lévy - Définition
En mathématiques, la constante de Lévy (quelquefois connue sous le nom constante de Khinchin-Lévy) apparaît dans une expression concernant le comportement asymptotique des dénominateurs convergents des fractions continuées. En 1936, le mathématicien français Paul Lévy montra que les dénominateurs
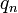
La constante de Lévy est la constante du côté droit de cette expression, et est approximativement égale à 3,275 822 918 7... Le terme est aussi quelquefois utilisé pour faire référence au logarithme du côté droit de cette expression, qui est approximativement égal à 1,186 569 110 4...