Triangulation de Delaunay - Définition
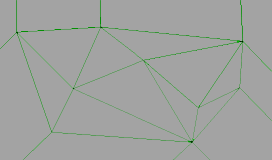
La triangulation de Delaunay d'un ensemble de n points est l'unique triangulation telle qu'un cercle passant par les trois points d'un triangle ne contienne aucun autre point. Cette notion peut être généralisée à n'importe quelle dimension : en 3D, par exemple, on utilisera des tétraèdres et des sphères.
La triangulation de Delaunay est le dual du diagramme de Voronoï, et possède donc des applications similaires.
On peut également définir la triangulation de Delaunay à partir de la construction (préalable) du diagramme de Voronoï des n mêmes points : cette triangulation est formée par l'ensemble des segments qui relient 2 des n points à condition qu'ils soient les centres de deux polygones adjacents du diagramme de Voronoï.
L'exemple suivant reprend les mêmes points que ceux de la page sur les diagrammes de Voronoï :
La triangulation porte le nom du mathématicien russe Boris Delone (1890 - 1980), francisé en Delaunay.

















































