Algèbre semi-simple - Définition

Analyse des endomorphismes

Anneau simple

Déterminons l'ensemble des endomorphismes dans un cas simple, celui de l'anneau A considéré comme un module sur lui-même. Un tel module est noté ici _AA. Une définition préalable est nécessaire :

• L'anneau opposé de A est l'anneau noté ici A^op muni de la multiplication définie par :

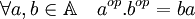
On dispose alors de la propriété suivante :

• L'ensemble des endomorphismes du module _AA est isomorphe à _AA^op.

Ce qui revient à dire que les endomorphismes correspondent à l'anneau opposé de A.

En effet, si φ est un endomorphisme, il est entièrement déterminé par l'image de 1. En effet, si a est un élément de A, alors son image est égal à a. φ(1), l'égalité suivante permet de conclure :

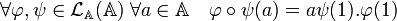
La structure d'anneau des endomorphisme est général aux algèbres, dans le cas d'une algèbre simple, le lemme de Schur indique que l'endomorphisme est soit nul, soit inversible ce qui démontre la propriété suivante :

• L'ensemble des endomorphismes d'une algèbre simple est un corps non nécessairement commutatif.

Dans le cas où l'algèbre simple est défini sur un corps commutatif algébriquement clos, les seuls automorphismes sont les homothéties.

• L'ensemble des endormorphismes d'une algèbre simple L sur un corps commutatif algébriquement clos K est isomorphe au centre de l'algèbre et à K.

Cette égalité s'écrit aussi : dim Hom_K^L(L, L) = 1. Cette égalité signifie que l'algèbre sur le corps K des endomorphismes de L en tant qu'algèbre est de dimension 1.

Algèbre simple

Soit l un élément de L non nul, on utilise la définition et de la proposition suivante :

• L'ensemble des éléments a de A tel que a.l est égal zéro est un idéal bilataire maximal, on l'appelle idéal annulateur de A car cet idéal est indépendant de l'élément l non nul choisi.

Soit a un élément de l'idéal annulateur de l. L'homothétie de rapport a possède un noyau non nul, le lemme de Schur indique alors que cette homothétie est l'application nulle. L'élément a annule tout élément de L, les annulateurs des différents éléments non nuls de L sont donc tous égaux. Cette propriété montre aussi que l'ensemble des éléments annulant l est un idéal à droite. Si b est un élément de A, alors b.a.l = b.0 = 0, l'annulateur est donc aussi un idéal à gauche. Montrons enfin qu'il est maximal, pour cela il suffit de remarquer que tout élément hors de l'annulateur est inversible. C'est encore une conséquence directe du lemme de Schur. Il est donc inutile de considérer le cas d'une algèbre simple sur un anneau, il suffit d'étudier celui d'une algèbre simple sur un corps, en général gauche.

• Le quotient de A par l'idéal annulateur est un corps inclus dans celui du corps opposé des endomorphismes d'une algèbre simple.

Ce quotient est composée d'éléments qui s'identifient à des homothéties inversibles, ce sont donc bien des endomorphismes. Une algèbre simple sur un corps est la donnée d'un anneau L simple et d'un sous-corps du corps de l'opposé de l'algèbre des endomorphismes de L. Pour cette raison, seules les algèbres simples sur un corps sont étudiées.

Propriétés héritées des modules

Une algèbre semi-simple est aussi un module semi-simple. En conséquence, une telle structure hérite directement de propriétés:

Caractérisation d'une algèbre semi-simple

• Les trois propositions suivantes sont équivalentes :

(i) L est une algèbre semi-simple.

(ii) L est somme de sous-algèbres simples.

(iii) Tout sous-algèbre est un facteur direct.

Les conséquences s'appliquent aussi aux algèbres :

• Supposons que L ne soit pas semi-simple, alors la somme de toutes les sous-algèbres simples de L est une sous-algèbre semi-simple, c'est la plus grande au sens de l'inclusion.

• Toute sous-algèbre d'une algèbre semi-simple est semi-simple.

Les démonstrations se trouvent dans l'article associés.

Lemme de Schur

Le lemme de Schur est un lemme technique explicitant la nature des morphismes entre une algèbre semi-simple et une algèbre simple. Il est à la fois simple à exprimer et à démontrer, cependant ses conséquences sont aussi nombreuses que profondes. Ici L désigne une algèbre semi-simple et S une algèbre simple sur A.

• Un morphisme de A dans L est soit nul soit injectif, un morphisme de L dans A est soit nul soit surjectif, si de plus L est simple alors un morphisme est soit nul soit bijectif. Si A est commutatif et si le polynôme minimal du morphisme est scindé, les seuls morphismes de S dans S sont les homothéties.

La structure d'un morphisme d'algèbres semi-simples est donc aisée à comprendre, elle correspond à une somme directe d'automorphismes de sous-algèbres simples et de morphisme nul.

Décomposition canonique

La décomposition d'une algèbre semi-simple en sous-algèbres simples n'est pas unique, pour obtenir une décomposition canonique, il est nécessaire de considérer la relation d'équivalence entre les sous-algèbres simples donnée par les isomorphismes. Deux algèbres simples sont en relation si et seulement s'il existe un isomorphisme de module entre elles. Soit N_i la somme des sous-algèbres d'une classe donnée. La décomposition suivante est canonique :

• N_i est la plus grande sous-algèbre ne contenant que des sous-algèbres simples isomorphes à S_i et toutes ses sous-algèbres sont isomorphes à S_i. L est somme directe des N_i.

• Avec les notations précédentes les sous-algèbres N_i sont appelées facteurs isotypiques de L.

Si une algèbre L ne contient que des sous-algèbre simples isomorphes deux à deux, alors l'algèbre L est qualifiée d'isotypique.

Le théorème d'Artin-Wedderburn énoncé ci-dessous, permet d'aller plus loin dans la compréhension de la structure.