Lemme de Schur - Définition

Introduction

En mathématiques et plus précisément en algèbre linéaire, le lemme de Schur est un lemme technique utilisé particulièrement dans la théorie de la représentation des groupes.

Il a été démontré en 1907 par Issai Schur dans le cadre de ses travaux sur la théorie des représentations d'un groupe fini,

Ce lemme est à la base de l'analyse d'un caractère d'une représentation d'un groupe fini. il permet, par exemple de caractériser les groupes abéliens finis.

Contexte

Motivation

Le lemme de Schur représente l'un des fondements de la théorie des représentations d'un groupe fini et de l'analyse de l'algèbre des modules semi-simples. Une représentation d'un groupe est la donnée d'un morphisme d'un groupe G dans l'ensemble des automorphismes d'un espace vectoriel. Cette approche initiée par Frobenius dans un article de 1896 s'avère fructueuse. Trois ans plus tard, Heinrich Maschke démontre que toute représentation est somme directe de représentations irréductibles.

Le lemme de Schur est un lemme technique essentiel pour la démonstration d'un résultat majeur : non seulement les représentations irréductibles s'identifient par leur caractère, mais en plus les caractères de ces représentations sont toutes orthogonales entre elles. Cette approche apporte des résultats majeurs pour la théorie des groupes finis. Elle a finalement permis la classification des groupes simples, mais aussi la démonstration de résultats comme une conjecture de William Burnside stipulant que tout groupe fini d'ordre impair est résoluble. Ce résultat est à l'origine de la Médaille Fields de Thompson .

Si ce lemme est aussi utilisé dans d'autres contextes, celui de la représentation est néanmoins le plus important.

Représentations d'un groupe fini

Rappelons la définition d'une représentation et fixons les notations pour le reste de l'article. G désigne ici un groupe fini d'ordre g. Son élément neutre est noté 1, et si s et t sont deux éléments de G la loi de composition interne du groupe sur s et t est noté st. E désigne un espace vectoriel sur un corps noté K.

• Une représentation du groupe G est la donnée d'un espace vectoriel E de dimension finie notée n et d'un morphisme de groupe ρ de G vers le groupe linéaire GL(E). Une représentation est notée (E, ρ) ou parfois et abusivement E.

C'est-à-dire que l'application ρ est à valeur dans l'espace des applications linéaires bijectives et préserve la loi du groupe, ce qui est équivalent à :

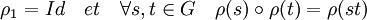
Théorème de Maschke

• Une représentation (V, ρ) est dite irréductible si et seulement si les seuls sous-espaces stables sont V et {0}.

La classification des représentation est une conséquence du théorème suivant connu sous le nom de théorème de Maschke:

• Si la caractéristique de K est première avec l'ordre de G, toute représentation (V, ρ) d'un groupe fini est somme directe de représentations irréductibles.

Connaître toutes les représentations d'un groupe fini revient donc à connaître ses représentation irréductibles, les autres s'obtiennent par somme directe.

Dans le cadre du lemme de Schur une définition plus légère suffit :

• Soit U une partie de L(E), l'ensemble des endomorphismes de E. U est dit irréductible s'il n'existe aucun sous-espace non trivial stable par tout élément de U.