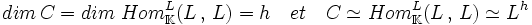Algèbre semi-simple - Définition
La liste des auteurs de cet article est disponible ici.
Théorème d'Artin-Wedderburn
Énoncé du théorème
Le théorème d'Artin-Wedderburn est au cœur de la structure de l'algèbre, il exprime de la manière suivante :
-
- Un anneau semi-simple tel que tout idéal simple est de dimension finie sur son corps d'endomorphismes, est isomorphe à un produit d'algèbres d'endomorphismes de modules de dimension fini sur des corps à priori distincts et gauches.
L'analyse des endomorphismes d'une algèbre simple montre que le théorème se généralise immédiatement aux algèbres semi-simples. Ainsi un algèbre simple correspond à un anneau d'endomorphismes de module sur un corps gauche, et une algèbre correspond à la même structure adjointe d'un sous-corps du corps gauche.
Réciproquement une généralisation d'un théorème de Burnside (cf paragraphe Démonstration de Burnside de l'article Théorème d'Artin-Wedderburn) montre que l'algèbre des endomorphismes d'un module sur un corps gauche adjointe de la multiplication externe naturelle sur un sous-corps du corps définissant le module est une algèbre simple. De plus, un produit fini d'algèbres simples est une algèbre semi-simple. La réciproque du théorème d'Artin-Wedderburn est donc vérifiée.
L'unicité de la structure est assurée par l'unicité de la décomposition d'un module semi-simple en facteurs isotypiques.
Dans le cas où A est un corps commutatif algébriquement clos, alors l'analyse précédente montre que les corps des algèbres des endomorphismes sont tous égaux à A. On bénéficie alors de la proposition suivante :
-
- Si A est un corps commutatif algébriquement clos et L une algèbre semi-simple de dimension finie n, alors la dimension de chaque facteur isotypique est un carré parfait di2. De plus l'égalité suivante est vérifiée si h désigne le nombre de sous-algèbres simples incluses dans L :
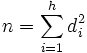
En effet, si di est la dimension d'un module simple Si de la i-ième composante isotypique de L, alors la i-ième algèbre est celle des endomorphisme de l'espace vectoriel sous-jacent de Si.
Centre de l'algèbre
Étudions le centre de l'algèbre dans le cas où l'algèbre est définie sur un corps commutatif algébriquement clos. Soient (Li) pour i variant de 1 à h la famille des sous-algèbres simples et c un élément du centre. Comme la famille des (Li) forme une somme directe égale à L, si l'on note pi le projecteur sur Li parallèlement à la somme directe des autres membres de la famille, on à l'égalité :
![c = \sum_{ij \in [1, h]} c_{ij} \quad avec \quad \forall i,j \in [1,h] \quad c_{ij}= p_j\circ c\circ p_i \;](https://static.techno-science.net/illustration/Definitions/autres/c/cdedc5c68ffdded699da75343ab386a8_abf322c356d14602a604ced8132ebc55.png)
Si i est différent de j, alors cij définit un morphisme de Li dans Lj. Le lemme de Schur indique qu'un tel morphisme est toujours nul. Si i est égal à j, alors cii correspond à un morphisme d'algèbre simple, c'est donc une homothétie d'un rapport à valeur dans K. En conclusion :
-
- Le centre de l'algèbre L est isomorphe à l'anneau somme directe d'autant de copies de K qu'il existe de sous-algèbres simples.
Cette égalité s'écrit maintenant si h désigne le nombre de sous-algèbres simples de l'algèbre L et C son centre.